初めに
本ページは、データの分析の相関関係、共分散、相関係数について、まとめます。今までは1変数に関してデータ分析をしてきましたが、このページでは、2変数の関係について学びます。
相関関係
用語解説
散布図
散布図:横軸と縦軸にそれぞれ別の量をとり、データが当てはまるところに点を打って示した(プロットした)グラフ
相関関係
- 2つのデータの一方が増えるとき、もう一方も増える傾向にある場合、正の相関関係があるという。
- 2つのデータの一方が増えるとき、もう一方が減る傾向にある場合、負の相関関係があるという。
- 2つのデータの間に、正の相関関係も負の相関関係もない場合、相関関係はないという。
散布図と相関関係
- 正の相関関係がある:右肩上がり
- 負の相関関係がある:右肩下がり
| 正の相関関係がある |  |
| 負の相関関係がある |  |
| 相関関係がない |  |
共分散、相関係数
共分散、相関係数の導出
2つの変数の相関を数値で表すために、具体例を用いて導出します。
5人の生徒に数学の小テストと英語の小テストの結果にどのような相関があるのか、分析してみましょう。
| 名前 | A | B | C | D | E | 計 |
| 数学の点数 | 2 | 4 | 6 | 8 | 10 | 30 |
| 英語の点数 | 3 | 6 | 7 | 9 | 10 | 35 |
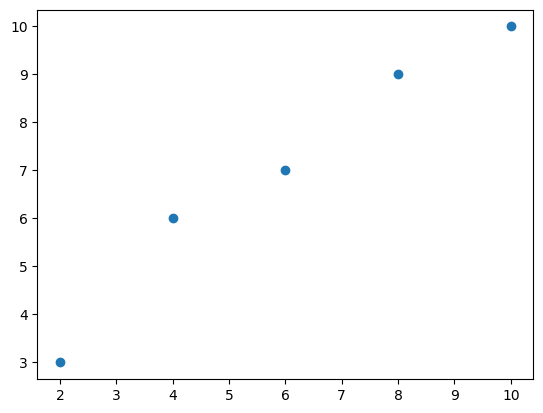
散布図をみると、正の相関関係があることが読み取れます。このデータの相関関係を数値で表すことを考えます。
数学の点数を\(x\)、英語の点数を\(y\)とし、\(x\)と\(y\)の平均値をそれぞれ\(\overline{x}\)、\(\overline{y}\)とします。すると、次が成り立つことがわかります。
- 正の相関関係があるならば、\((x – \overline{x})(y – \overline{y}) > 0\)が成り立つデータが多い。
- 負の相関関係があるならば、\((x – \overline{x})(y – \overline{y}) < 0\)が成り立つデータが多い。
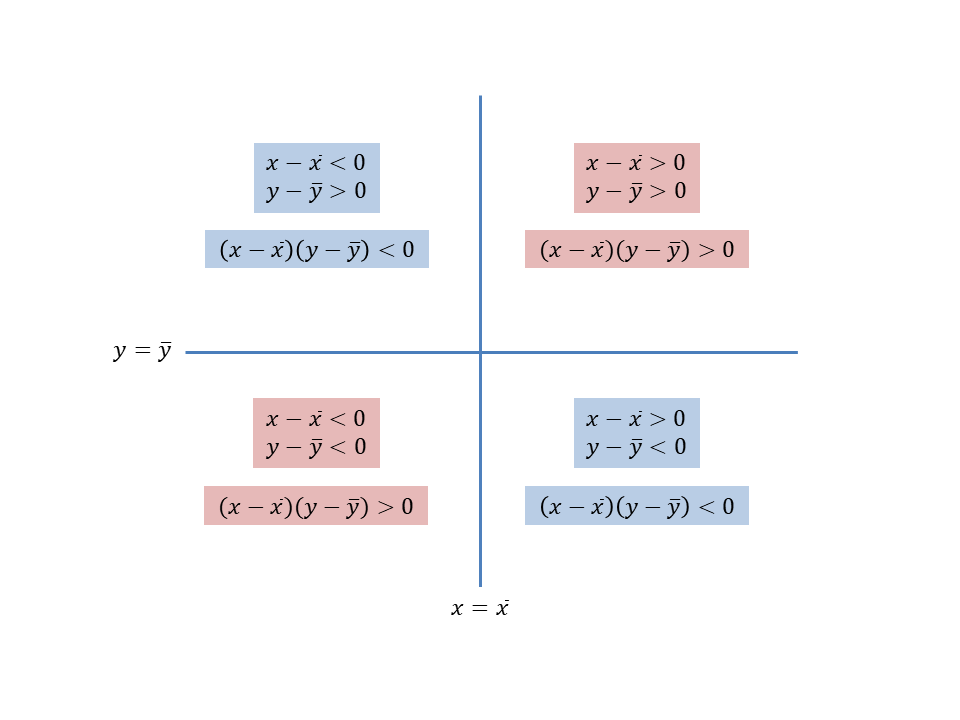
そこで、相関関係を調べるために偏差の積の平均値\(s_{xy}\)を求めてみます。\(s_{xy} > 0\)であれば正の相関関係があり、\(s_{xy} < 0\)であれば、負の相関関係があるでしょう。
いま、\(\overline{x} = \frac{30}{5} = 6, \overline{y} = \frac{35}{5} = 7\)となります。よって、
\[\begin{align}
&s_{xy} \\
= &\frac{(2 – 6)(3 – 7) + (4 – 6)(6 – 7) + (6 – 6)(7 – 7) + (8 – 6)(9 – 7) + (10 – 6)(10 – 7)}{5} \\
= &\frac{16 + 2 + 0 + 4 + 12}{5} \\
= &\frac{34}{5} \\
= &6.8
\end{align}\]
この偏差の積の平均値\(s_{xy}\)を\(x\)と\(y\)の共分散といいます。
さて、先ほどのデータを100倍したデータの共分散を考えてみましょう。
| 名前 | A | B | C | D | E | 計 |
| 数学の点数 \(\times 100\) | 200 | 400 | 600 | 800 | 1000 | 3000 |
| 英語の点数 \(\times 100\) | 300 | 600 | 700 | 900 | 1000 | 3500 |
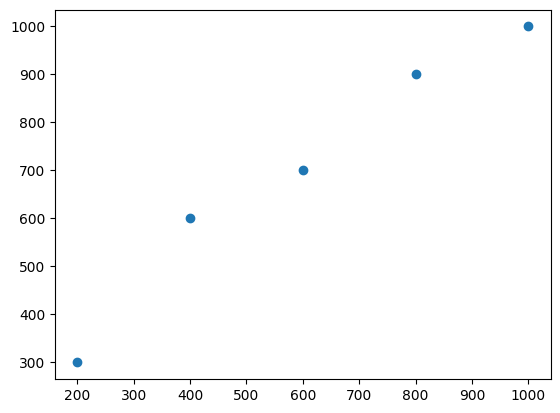
散布図から読み取れるように、元のデータと100倍した後のデータに関して、数学の点数と英語の点数の関係性は同じです。100倍した点数の平均値はそれぞれ\(600, 700\)であり、共分散は次のようになります。
\[\begin{align}
&\frac{(200 – 600)(300 – 700) + (400 – 600)(600 – 700) + \cdots + (10 – 6)(10 – 7)}{5} \\
= &\frac{160000 + 20000 + 0 + 40000 + 120000}{5} \\
= &\frac{340000}{5} \\
= &68000
\end{align}\]
2つのデータの値が100倍になっただけで、データの関係性は変化していないにもかかわらず、もともとの共分散の\(10000\)倍になりました。つまり、共分散はデータの関係性だけでなく、データの値の大きさに左右されるということです。
共分散を\(x\)、\(y\)の標準偏差\(s_x, s_y\)で割ることでデータの値の大きさに左右されないように補正することができます。
| 名前 | A | B | C | D | E | 計 |
| 数学の点数 \(x\) | 2 | 4 | 6 | 8 | 10 | 30 |
| 英語の点数 \(y\) | 3 | 6 | 7 | 9 | 10 | 35 |
| \(x – \overline{x}\) | -4 | -2 | 0 | 2 | 4 | 0 |
| \((x – \overline{x})^2\) | 16 | 4 | 0 | 4 | 16 | 40 |
| \(y – \overline{y}\) | -4 | -1 | 0 | 2 | 3 | 0 |
| \((y – \overline{y})^2\) | 16 | 1 | 0 | 4 | 9 | 30 |
\(s_x = \sqrt{\frac{40}{5}} = \sqrt{8}\)、\(s_y = \sqrt{\frac{30}{5}} = \sqrt{6}\)です。よって、
\[
\frac{s_{xy}}{s_x s_y} = \frac{6.8}{\sqrt{8} \sqrt{6}} = \frac{1.7 \sqrt{3}}{3} \ \unicode{x2252} \ 0.98
\]
となります。この\(\frac{s_{xy}}{s_x s_y}\)を相関係数といいます。
100倍したデータの相関係数も同じように求めてみましょう。
| 名前 | A | B | C | D | E | 計 |
| 数学の点数 \(x \times 100\) | 200 | 400 | 600 | 800 | 1000 | 3000 |
| 英語の点数 \(y \times 100\) | 300 | 600 | 700 | 900 | 1000 | 3500 |
| \(100x – \overline{100x}\) | -400 | -200 | 0 | 200 | 400 | 0 |
| \((100x – \overline{100x})^2\) | 1600 | 400 | 0 | 400 | 1600 | 4000 |
| \(100y – \overline{100y}\) | -400 | -100 | 0 | 200 | 300 | 0 |
| \((100y – \overline{100y})^2\) | 1600 | 100 | 0 | 400 | 900 | 3000 |
標準偏差はそれぞれ\(\sqrt{\frac{4000}{5}} = \sqrt{800} = 100\sqrt{8}\)、\(\sqrt{\frac{3000}{5}} = \sqrt{600} = 100\sqrt{6}\)になります。よって、相関係数は
\[
\frac{68000}{100\sqrt{8} \times 100\sqrt{6}} = \frac{6.8}{\sqrt{8} \sqrt{6}} = \frac{1.7 \sqrt{3}}{3} \ \unicode{x2252} \ 0.98
\]
となりました。相関係数は共分散と違い、データの値の大きさに左右されず、等しい値を算出されました。
用語解説
共分散
2つの変数\(x, y\)について、\(n\) 個の値の組 \((x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)\) を考える。また、\(x, y\) の平均値をそれぞれ \(\overline{x}, \overline{y}\) とする。このとき
\[
s_{xy} = \frac{1}{n} \left\{ (x_1 – \overline{x})(y_1 – \overline{y}) + (x_2 – \overline{x})(y_2 – \overline{y}) + \cdots + (x_n – \overline{x})(y_n – \overline{y})\right\}
\]
を \(x\) と \(y\) の共分散という。
相関係数
2つの変数 \(x, y\) の標準偏差をそれぞれ \( s_x, s_y \) とする。また、\(x\) と \(y\) の共分散を \(s_{xy}\) とする。このとき、
\[
r = \frac{s_{xy}}{s_x s_y}
\]
を \(x\) と \(y\) の相関係数という。
相関係数 \(r\) は次の性質をもつ。
- \(-1 \leq r \leq 1\)
- \(r\) の値が \(1\) に近いほど、正の相関関係が強い
- \(r\) の値が \(-1\) に近いほど、負の相関関係が強い
- \(r\) の値が \(0\) に近いほど、相関は弱くなる。
例題
問題
次のような5人の身長と体重のデータがある。
| 名前 | 身長(cm) | 体重(kg) |
| A | 168 | 60 |
| B | 177 | 72 |
| c | 171 | 66 |
| D | 165 | 54 |
| E | 174 | 68 |
| 計 | 855 | 320 |
このデータの身長 \(x\) と体重 \(y\) の相関係数を求め、相関関係を調べよ。ただし、\(\sqrt{5} = 2.24\) としてよい。
解答
\(x, y\) の平均値 \(\overline{x}, \overline{y}\) はそれぞれ次のようになる。
\[\begin{align}
\overline{x} &= \frac{855}{5} = 171 \\
\overline{y} &= \frac{320}{5} = 64 \\
\end{align}\]
| 名前 | \(x\)(cm) | \(y\)(kg) | \(x – \overline{x}\) | \(y – \overline{y}\) | \((x – \overline{x})^2\) | \((y – \overline{y})^2\) | \((x – \overline{x})(y – \overline{y})\) |
| A | 168 | 60 | -3 | -4 | 9 | 16 | 12 |
| B | 177 | 72 | 6 | 8 | 36 | 64 | 48 |
| c | 171 | 66 | 0 | 2 | 0 | 4 | 0 |
| D | 165 | 54 | -6 | -10 | 36 | 100 | 60 |
| E | 174 | 68 | 3 | 4 | 9 | 16 | 12 |
| 計 | 855 | 320 | 0 | 0 | 90 | 200 | 132 |
したがって、\(x\) の標準偏差 \(s_x\) と \(y\) の標準偏差 \(s_y\)、\(x\) と \(y\) の共分散 \(s_{xy}\)はそれぞれ次のようになる。
\[\begin{align}
s_x &= \sqrt{\frac{90}{5}} = \sqrt{18} = 3 \sqrt{2} \\
s_y &= \sqrt{\frac{200}{5}} = \sqrt{40} = 2 \sqrt{10}\\
s_{xy} &= \frac{132}{5} = 26.4
\end{align}\]
よって、\(x\) と \(y\) の相関係数 \(r\) は
\[
r = \frac{s_{xy}}{s_x s_y} = \frac{26.4}{3 \sqrt{2} \times 2 \sqrt{10}} = \frac{26.4}{12 \sqrt{5}} = \frac{26.4 \sqrt{5}}{60} = 0.44 \times 2.24 = 0.9856
\]
補足
相関係数の求め方
相関係数の定義は \(r = \frac{s_{xy}}{s_x s_y}\) であり、先ほどの例題も定義をそのまま用いて、解答を求めた。しかし
\[\begin{align}
& \frac{s_{xy}}{s_x s_y} \\
= &\frac{\frac{1}{n} \left\{ (x_1 – \overline{x})(y_1 – \overline{y}) + \cdots + (x_n – \overline{x})(y_n – \overline{y}) \right\}}{\sqrt{\frac{1}{n} \left\{ (x_1 – \overline{x})^2 + \cdots + (x_n – \overline{x})^2\right\}}\sqrt{\frac{1}{n} \left\{ (y_1 – \overline{y})^2 + \cdots + (y_n – \overline{y})^2\right\}}} \\
= &\frac{(x_1 – \overline{x})(y_1 – \overline{y}) + \cdots + (x_n – \overline{x})(y_n – \overline{y})}{\sqrt{ (x_1 – \overline{x})^2 + \cdots + (x_n – \overline{x})^2} \sqrt{(y_1 – \overline{y})^2 + \cdots + (y_n – \overline{y})^2}}
\end{align}\]
が成り立つため、上記の例では次のように相関係数を求めることができる。
\[
r = \frac{132}{\sqrt{90} \sqrt{200}} = \frac{132}{60 \sqrt{5}} = \frac{132 \sqrt{5}}{300} = 0.44 \times 2.24 = 0.9856
\]
相関係数の絶対値が1以下になる理由
相関係数 \(r\) が \(-1 \leq r \leq 1\) を満たす理由は次の不等式が成り立つからです。
\[
({a_1}^2 + \cdots + {a_n}^2)({b_1}^2 + \cdots + {b_n}^2) \geq (a_1 b_1 + \cdots + a_n b_n)^2
\]
この不等式はコーシーシュワルツの不等式と呼ばれるものです。
コーシーシュワルツの不等式に関して、\(a_i = x_i – \overline{x}, b_i = y_i – \overline{y}\) とすると
\[\begin{align}
({a_1}^2 + \cdots + {a_n}^2)({b_1}^2 + \cdots + {b_n}^2) &\geq (a_1 b_1 + \cdots + a_n b_n)^2 \\
\frac{1}{n} ({a_1}^2 + \cdots + {a_n}^2) \times \frac{1}{n}({b_1}^2 + \cdots + {b_n}^2) & \geq \frac{1}{n^2} (a_1 b_1 + \cdots + a_n b_n)^2 \\
{s_x}^2 {s_y}^2 & \geq {s_{xy}}^2 \ (\because n > 0)
\end{align}\]
となります。よって、\(r^2 \leq 1\) より \(-1 \leq r \leq 1\) を示すことができます。
コーシーシュワルツの不等式の証明は数学Ⅰの範囲内で可能ですが、数学Bの数列で学ぶ \(\sum\) を使った方が簡潔に書けるため、ここでは割愛します。


