初めに
本記事では、高校数学の数学Ⅰの単元の1つであるデータの分析で学ぶ度数分布表、ヒストグラム、代表値についてまとめます。
度数分布表とヒストグラム
用語解説
階級
階級:データの値の範囲
階級値
階級値:各階級の中央の値
度数
度数:各階級に含まれるデータの個数
相対度数
相対度数:各階級の度数の全体に対する割合
累積相対度数
累積相対度数:その階級までの相対度数の総和
ヒストグラム
ヒストグラム:横軸に階級、縦軸に度数をとり、各階級の度数を示した柱状グラフ
例題
問題
ある10人の生徒に数学のテストを実施した結果が次のようになった。
23 51 88 40 66 38 58 62 71 49 (点)
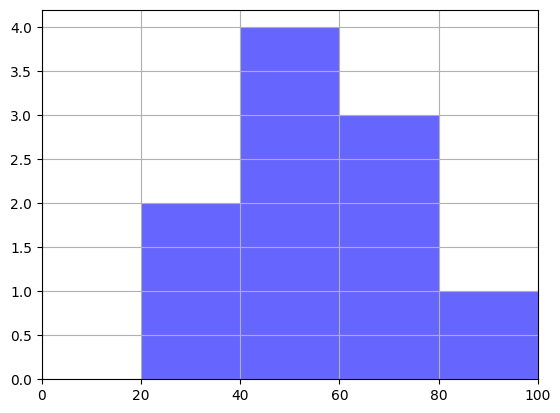
このテストの結果を階級の幅を20点とし、階級値、度数、相対度数、累積相対度数の度数分布表を作成せよ。また、ヒストグラムに表せ。
解答
| 階級(点) | 階級値(点) | 度数(人) | 相対度数 | 累積相対度数 |
| 0以上~20未満 | 10 | 0 | 0 | 0 |
| 20 ~40 | 30 | 2 | 0.2 | 0.2 |
| 40 ~60 | 50 | 4 | 0.4 | 0.5 |
| 60 ~80 | 70 | 3 | 0.3 | 0.9 |
| 80 ~100以下 | 90 | 1 | 0.1 | 1 |
度数分布表は上のようになる。また、ヒストグラムは下図のようになる。
解説
階級値は各階級の中央の値です。相対度数はデータの大きさが10であるので、次のように求められます。
\[
\text{相対度数} = \frac{\text{度数}}{データの大きさ} = \frac{\text{度数}}{10}
\]
度数分布表、ヒストグラムに整理する意義
上記の例題で、10人の生徒に数学のテストの結果についての度数分布表とヒストグラムを作成しました。
23 51 88 40 66 38 58 62 71 49 (点)
| 階級(点) | 階級値(点) | 度数(人) | 相対度数 | 累積相対度数 |
| 0以上~20未満 | 10 | 0 | 0 | 0 |
| 20 ~40 | 30 | 2 | 0.2 | 0.2 |
| 40 ~60 | 50 | 4 | 0.4 | 0.5 |
| 60 ~80 | 70 | 3 | 0.3 | 0.9 |
| 80 ~100以下 | 90 | 1 | 0.1 | 1 |

元データは整理されておらず、データの特徴が読み取りづらいので、それを階級ごとに整理したものが度数分布表です。これで少し分かりやすくなりました。しかし、度数分布表もちゃんと理解しようとしなければ、特徴が読み取れないため、視覚的にわかるようにグラフ化したものがヒストグラムです。
元データより表、表よりグラフのほうが直感的に理解がしやすいと思います。
代表値
用語解説
代表値
代表値:データ全体の特徴を表す数値。平均値、中央値、最頻値がある。
平均値
\( n \) 個のデータの値を \( x_1, x_2, \cdots, x_n \) とするとき, これらの平均値 \( \overline{x} \) を次で定義する。
\[
\overline{x} = \frac{1}{n} (x_1 + x_2 + \cdots + x_n)
\]
データの値の総和をデータの個数で割ったものが平均値である。
中央値
中央値:データを値の小さい順に並べたときび中央の値
ただし、データの個数 \(n\) が奇数の時は、ちょうど真ん中(\( \frac{n + 1}{2} \) 個目)の値を中央値とし、データの個数 \(n\) が偶数の時は、真ん中の2つの値(\( \frac{n}{2} \) 個目と \( \frac{n}{2} + 1\) 個目の値)の平均値を中央値とする。
奇数個の場合:〇〇〇〇〇 〇が中央値
偶数個の場合:〇〇〇〇〇〇 2つの〇の平均値が中央値
最頻値(モード)
最頻値:最も個数の多い値
ただし、度数分布表のみ与えられている場合は、最も度数が多い階級の階級値を最頻値とする。
例題1
問題
次のデータの値の平均値、中央値、最頻値を求めよ。
4, 10, 10, 11, 13, 15, 21
解答
平均値は \( \frac{1}{7} (4 + 10+ 10 + 11 + 13 + 15 + 21) = \frac{84}{7} = 12 \)
中央値は \(11\)、最頻値は \(10\) である。
解説
平均値は定義通りに計算しています。中央値は小さい順に並べたときに中央の値なので\(11\)である。最頻値は個数が最も多い値なので\(10\) となる。
例題2
問題
次のデータの値の中央値を求めよ。
9, 1, 11, 8, 6, 16
解答
小さい順に並べると\(1, 6, 8, 9, 11, 16\)となる。よって、中央値は\(\frac{8 + 9}{2} = \frac{17}{2} = 8.5\) となる。
例題3
問題
次の値の平均値を求めよ。
512, 502, 495, 499, 509, 495
解答
\[
500 + \frac{1}{6}(12 + 2 – 5 – 1 + 9 – 5) = 500 + \frac{12}{6} = 502
\]
よって、求める平均値は\(502\)である。
解説
仮平均を使って求めている。
\[\begin{align}&\frac{1}{6} (512 + 502 + 495 + 499 + 509 + 495) \\ = &\frac{1}{6} \{500 \times 6 + (12 + 2 – 5 – 1 + 9 – 5)\} \\ = &500 + \frac{1}{6}(12 + 2 – 5 – 1 + 9 – 5) \\ = & \cdots \end{align}\]
上の式では、すべての値が\(500\)に近いため、\(500\)を先に計算し、数値を小さくしてから平均値を求める。このときの\(500\)に該当する数値を仮平均という。仮平均は自分で計算しやすい値に設定してよい。
代表値の使い分け
代表値は、次のように使い分けをします。
- 平均値:データの全体的な傾向を把握したい場合
- 中央値:外れ値の影響を受けにくい代表値を知りたい場合や、データの分布が非対称な場合
- 最頻値:データの集中傾向を知りたい場合
平均値はデータの全体的な傾向を把握できますが、外れ値の影響を受けやすいという欠点があります。
例えば、5人の小学生の月額のお小遣いのデータが次のようになっているとします。
100 500 600 300 100000 (円)
このとき、この5人のお小遣いの平均値は\(\frac{1}{5}(100 + 500 + 600 + 300 + 100000 = 20300\)円となります。これは明らかに外れ値である\(100000\)円の影響を大きく受けており、元データの全体の特徴を表しているとは言い難いです。
こういった外れ値があるデータの場合は、中央値が適切です。このデータの中央値は\(500\)円であり、外れ値の影響を受けずに値をだすことができます。
最頻値は、最も度数の大きい値を調べられます。ヒストグラムでは山が最も高い部分の値をとります。例えば、商品の販売個数を調べるときに最も売れた商品を知りたければ最頻値を求めることになります。