初めに
このページでは、数学Ⅰのデータの分析で学ぶ偏差、分散、標準偏差についてまとめます。これらはデータの散らばり度合いを示す数値です。
偏差、分散、標準偏差
分散、標準偏差の導出
Aさん、Bさん、\(\cdots\)、Jさんの10人を5人ずつに分け、数学のテストを実施しました。次のような結果が得られたとします。
| 名前 | A | B | C | D | E | 計 |
| 点数\(x\) | 56 | 73 | 91 | 42 | 63 | 325 |
| 名前 | E | F | G | H | I | 計 |
| 点数\(y\) | 61 | 69 | 57 | 76 | 62 | 325 |
グループ1とグループ2の点数の平均点はどちらも\(325 \div 5 = 65\)点ですが、実際の点数をみるとグループ1のほうがグループ2より平均点から散らばっているように見えます。ここで、それぞれのデータの平均点からの散らばりの度合いを調べることを考えます。
平均点からの散らばりの度合いを調べるために、平均点からの差に着目し、その平均をとってみることにします。平均点からの差を平均点からの偏差といいます。
グループ1の平均点を\(\overline{x}\)、グループ2の平均点を\(\overline{y}\)とすると、\(\overline{x} = \overline{y}= 65\)です。
| 名前 | A | B | C | D | E | 計 |
| 点数\(x\) | 56 | 73 | 91 | 42 | 63 | 325 |
| \(x – \overline{x}\) | -9 | 8 | 26 | -23 | -2 | 0 |
| 名前 | F | G | H | I | J | 計 |
| 点数\(y\) | 61 | 69 | 57 | 76 | 62 | 325 |
| \(y – \overline{y}\) | -4 | 4 | -8 | 11 | -3 | 0 |
上の表から平均点からの偏差の総和は正の数と負の数が相殺しあって、どちらも\(0\)となることがわかります。そのため、平均点からの差の平均も\(0\)になり、単純に差をとると散らばりの度合いが分かりません。
そこで、すべての値を\(0\)以上にするために、平均点からの偏差を\(2\)乗したものを考えます。
| 名前 | A | B | C | D | E | 計 |
| 点数\(x\) | 56 | 73 | 91 | 42 | 63 | 325 |
| \(x – \overline{x}\) | -9 | 8 | 26 | -23 | -2 | 0 |
| \((x – \overline{x})^2\) | 81 | 64 | 676 | 529 | 4 | 1354 |
| 名前 | F | G | H | I | J | 計 |
| 点数\(y\) | 61 | 69 | 57 | 76 | 62 | 325 |
| \(y – \overline{y}\) | -4 | 4 | -8 | 11 | -3 | 0 |
| \((y – \overline{y})^2\) | 16 | 16 | 64 | 121 | 9 | 226 |
この表より
\[
\begin{align}
\text{グループ1の偏差の2乗の平均値} &= \frac{1354}{5} = 264.8 \\
\text{グループ2の偏差の2乗の平均値} &= \frac{226}{5} = 45.8
\end{align}
\]
が得られます。したがって、\(264.8 > 45.8\)より平均点からの散らばりの度合いが大きいのはグループ1であったことが分かります。
いま求めた平均値からの偏差の\(2\)乗の平均値を分散といいます。
分散は、平均値からの偏差の\(2\)乗の平均値であるため、元のデータと単位がそろっていません。今回であれば元のデータの単位は(点)ですが、分散の単位は(\(\text{点}^2\))となっています。本来は、平均点\(65\)から\(7\)点離れているといったように表現したいものです。そこで、分散に平方根をつけ、単位を合わせてみます。
\[
\begin{align}
\sqrt{\text{グループ1の偏差の2乗の平均値}} &= \sqrt{264.8} \ \unicode{x2252}\ 16.27\\
\sqrt{\text{グループ2の偏差の2乗の平均値}} &= \sqrt{45.8} \ \unicode{x2252} \ 6.77
\end{align}
\]
これで、グループ1は平均点から約\(16.27\)点、グループ2は平均点から約\(6.77\)点分散らばっていることを示すことができました。
この分散の正の平方根を標準偏差といいます。
用語解説
偏差
偏差:基準値(平均値、中央値など)との差
変数\(x\)の取る値が\(x_1, x_2, \cdots, x_n\)であり、\(x\)の平均値を\(\overline{x}\)とする。このとき、
\[
x_1 \ – \ \overline{x}, x_2 \ – \ \overline{x}, \cdots, x_n \ – \ \overline{x}
\]
を、それぞれ平均値からの偏差という。
分散、標準偏差
変数\(x\)のとる値が\(x_1, x_2, \cdots, x_n\)であり、\(x\)の平均値を\(\overline{x}\)とする。このとき、偏差の\(2\)乗の平均値
\[
s^2 = \frac{1}{n} \left\{(x_1 \ – \ \overline{x})^2 + (x_2 \ – \ \overline{x})^2 + \cdots + (x_n \ – \ \overline{x})^2) \right\}
\]
を\(x\)の分散という。また、分散\(s^2\)の正の平方根
\[
s = \sqrt{s^2} = \sqrt{\frac{1}{n} \left\{(x_1 \ – \ \overline{x})^2 + (x_2 \ – \ \overline{x})^2 + \cdots + (x_n \ – \ \overline{x})^2) \right\}}
\]
を\(x\)の標準偏差という。
偏差を\(2\)乗する理由の補足
分散の導出の中で、偏差の総和は正の数と負の数が相殺しあって、どちらも\(0\)となるため、すべての値を\(0\)以上にするために、偏差の\(2\)乗をしました。しかし、\(0\)以上にする方法として、絶対値をとるという方法も考えられます。実は、絶対値をとらず、\(2\)乗をした理由はもう1つあります。
分散は散らばりの度合いの2乗を、標準偏差は散らばりの度合いを表していますが、散らばりの度合いは平均値からの距離とみることもできます。
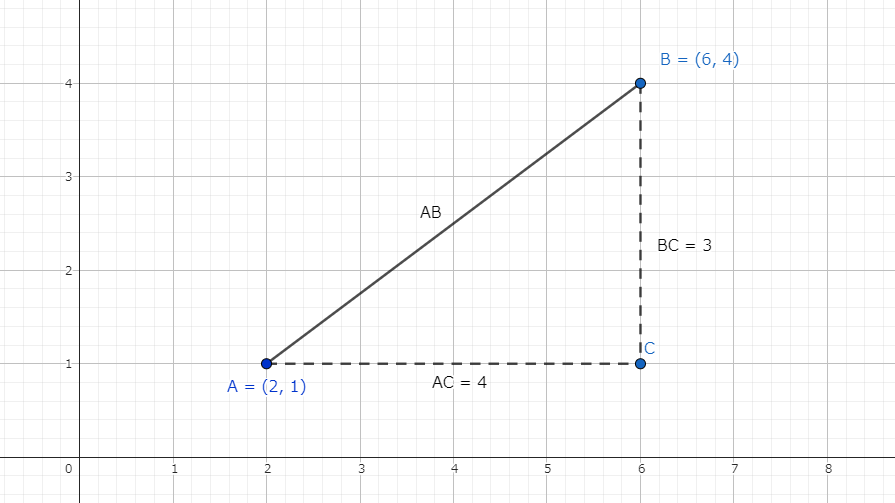
ここで2点間の距離の求め方を思い出してみましょう。
2点\(\rm{A}(2, 1), \rm{B}(6, 4)\)の距離を求めると
\[\begin{align}
\rm{AB}^2 &=(6 \ – \ 2)^2 + (4 \ – \ 1)^2 \\
\rm{AB} &= \sqrt{(6 \ – \ 2)^2 + (4 \ – \ 1)^2} \\
\rm{AB} &= 5
\end{align}
\]
となります。これを見ると\(\rm{AB}^2 = (6 – 2)^2 + (4 – 1)^2\)は分散と同じ形をしており、\(\rm{AB} = \sqrt{(6 – 2)^2 + (4 – 1)^2}\)は標準偏差を同じ形をしていることが分かります。
分散を定義するときに、偏差の絶対値の平均値ではなく、偏差の\(2\)乗の平均値としたのは、距離の求め方と同じにしたかったという理由があります。
分散の公式
公式
変数\(x\)の平均値を\(\overline{x}\)、\(x^2\)の平均値を\(\overline{x^2}\)とする。このとき、\(x\)の分散\(s^2\)は次で求められる。
\[
s^2 = \overline{x^2} \ – \ (\overline{x})^2
\]
証明
変数\(x\)のとる値を\(x_1, x_2, \cdots, x_n\)とする。このとき、
\[\begin{align}
s^2 &= \frac{1}{n} \left\{(x_1 \ – \ \overline{x})^2 + (x_2 \ – \ \overline{x})^2 + \cdots + (x_n \ – \ \overline{x})^2) \right\} \\
&= \frac{1}{n} \left\{({x_1}^2 + {x_2}^2 + \cdots + {x_n}^2) – 2(x_1 + x_2 + \cdots + x_n) \overline{x} + n (\overline{x})^2 \right\} \\
&= \frac{1}{n} ({x_1}^2 + {x_2}^2 + \cdots + {x_n}^2) – \frac{2}{n}(x_1 + x_2 + \cdots + x_n) \overline{x} + (\overline{x})^2 \\
&= \overline{x^2} \ – \ 2(\overline{x})^2 + (\overline{x})^2 \\
&= \overline{x^2} \ – \ (\overline{x})^2
\end{align}\]
例題
問題
あるクラスで小テストを実施したところ次のような結果になった。
| 名前 | A | B | C | D | E | F | G |
| 点数 | 8 | 6 | 10 | 4 | 7 | 5 | 9 |
このデータについて、分散と標準偏差を求めよ。
解答(定義通り)
このデータの平均点は\(\frac{1}{7}(8 + 6 + 10 + 4 + 7 + 5 + 9) = \frac{49}{7} = 7\)である。
| 名前 | A | B | C | D | E | F | G | 計 |
| 点数 | 8 | 6 | 10 | 4 | 7 | 5 | 9 | 49 |
| 偏差 | 1 | -1 | 3 | -3 | 0 | -2 | 2 | 0 |
| 偏差の\(2\)乗 | 1 | 1 | 9 | 9 | 0 | 4 | 4 | 28 |
よって、分散は\(\frac{28}{7} = 4\)であり、標準偏差は\(\sqrt{4} = 2\)である。
解答(公式)
| 名前 | A | B | C | D | E | F | G | 計 |
| 点数 | 8 | 6 | 10 | 4 | 7 | 5 | 9 | 49 |
| 点数の\(2\)乗 | 64 | 36 | 100 | 16 | 49 | 25 | 81 | 371 |
よって、平均値は\(\frac{49}{7} = 7\)、\(2\)乗の平均値は\(\frac{371}{7} = 53\)である。よって、分散は\(53 – 7^2 = 4\)であり、標準偏差は\(\sqrt{4} = 2\)である。