初めに
本記事は場合の数と確率の準備として、集合の要素の個数について、まとめます。オイラー図を用いて要素の個数を考えられるようになることを優先して学びましょう。
集合の要素の個数
用語解説
集合の要素の個数
\(A\) を集合とする。このとき、\(A\) の要素の個数を \(n(A)\) と表す。
和集合・共通部分
全体集合を \(U\) とする。集合 \(A, B\) において、
\(A\) と \(B\) の共通部分 \(A \cap B\):\(A\) と \(B\) のどちらにも属する要素の集合。\(A\) かつ \(B\) とよぶ。
\(A\) と \(B\) の和集合 \(A \cup B\) :\(A\) と \(B\) の少なくとも一方に属する要素の集合。\(A\) または \(B\) とよぶ。
| \(A \cap B\) | \(A \cup B\) |
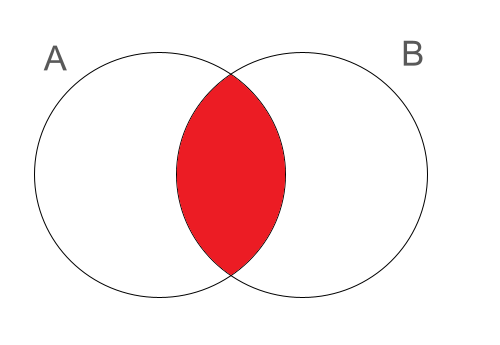 |  |
オイラー図・ベン図
オイラー図:集合の相関関係を表す図
ベン図:オイラー図の中で集合をすべての交差を示したもの
ベン図はオイラー図であるが、オイラー図は必ずしもベン図ではありません。
| ベン図の例 | オイラー図であるがベン図ではないものの例 |
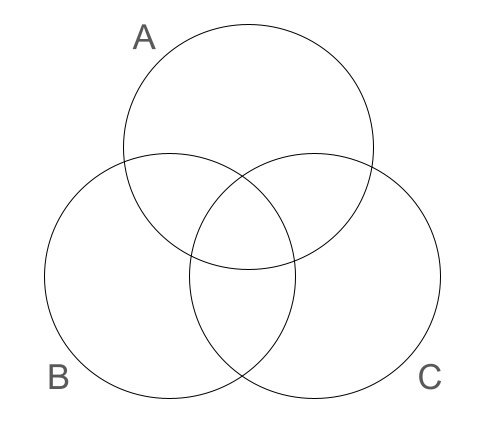 | 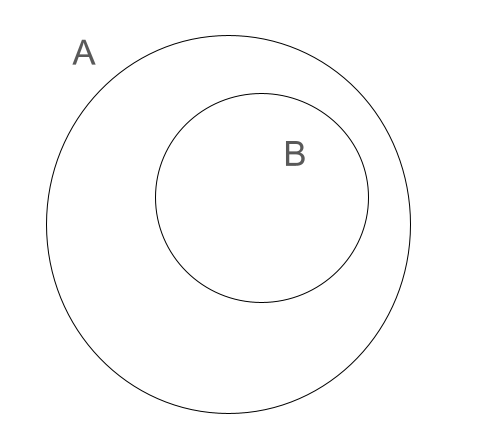 |
補集合
全体集合を \(U\) とする。集合 \(A\) に対して、\(U\) の要素であり \(A\) の要素でないものの全体の集合を \(A\) の補集合といい、\(\overline{A}\) で表す。
公式・法則
2つの集合の和集合の公式
集合 \(A, B\) に関して次が成り立つ。
\[\begin{align}
n(A \cup B) = &n(A) + n(B) \ – \ n(A \cap B)
\end{align}\]
3つの集合の和集合の公式
集合 \(A, B, C\) に関して次が成り立つ。
\[\begin{align}
&n(A \cup B \cup C) \\
= &n(A) + n(B) + n(C) \ – \ n(A \cap B) \ – \ n(B \cap C) \ – \ n(C \cap A) + n(A \cap B \cap C)
\end{align}\]
ド・モルガンの法則
集合 \(A, B\) において、次が成り立つ。
\[\begin{align}
\overline{A \cap B} &= \overline{A} \cup \overline{B} \\
\overline{A \cup B} &= \overline{A} \cap \overline{B}
\end{align}\]
例題1
問題
\(A = \{2, 5, 8, 13, 17\}\) の要素の個数 \(n(A)\) を求めよ。
解答
\(n(A) = 5\)
例題2
問題
100以下の自然数のうち、2の倍数または3の倍数の個数を求めよ。
解答
全体集合 \(U = \{1, 2, \cdots, 100\}\) とし、2の倍数の集合を \(A\)、3の倍数の集合を \(B\) とする。\(n(A \cup B)\) を求めればよい。
\(100 \div 2 = 50, 100 \div 3 = 33 \text{余り} 1\) より
\[n(A) = 50, n(B) = 33\]
である。また、\(A \cap B\) は6の倍数であり \(100 \div 6 = 16 \text{余り} 4\) より
\[n(A \cap B) = 16\]
である。よって、
\[
n(A \cup B) = n(A) + n(B) \ – \ n(A \cap B) = 50 + 33 \ – \ 16 = 67
\]
となる。以上より求める個数は67個。
練習問題
問題
100人の生徒に通学方法を聞いたところ、自転車を使う人が53人、電車を使う人が30人、どちらも使わない人が24人であった。自転車も電車も使う人の人数を求めよ。
解答
全体集合である100人の生徒の集合を \(U\) とし、自転車を使う人の集合を \(A\)、電車を使う人の集合を \(B\) とする。
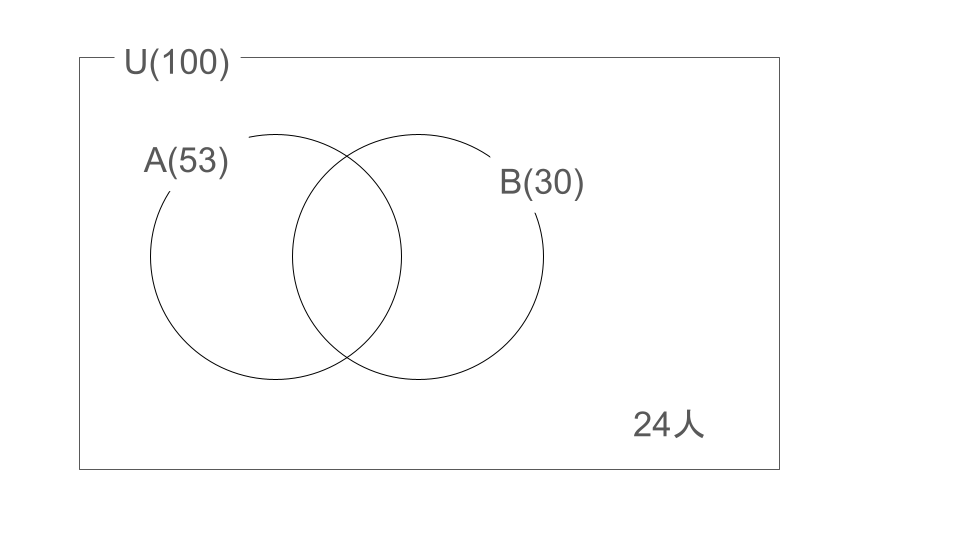
このとき、どちらも使わない人が24人であるため、\(n(\overline{A \cup B}) = 24\) となる。よって、
\[
n(A \cup B) = n(U) \ – \ n(\overline{A \cup B}) = 100 \ – \ 24 = 76
\]
となる。したがって、\(n(A \cup B) = n(A) + n(B) \ – \ n(A \cap B)\) より
\[\begin{align}
76 &= 50 + 33 \ – \ n(A \cap B) \\
n(A \cap B) &= 50 + 33 \ – \ 76 \\
n(A \cap B) &= 7
\end{align}\]
以上より、自転車も電車も使う人の人数は7人。



