初めに
本記事は、場合の数で必要な知識を網羅的に学びます。
場合の数
用語解説
樹形図
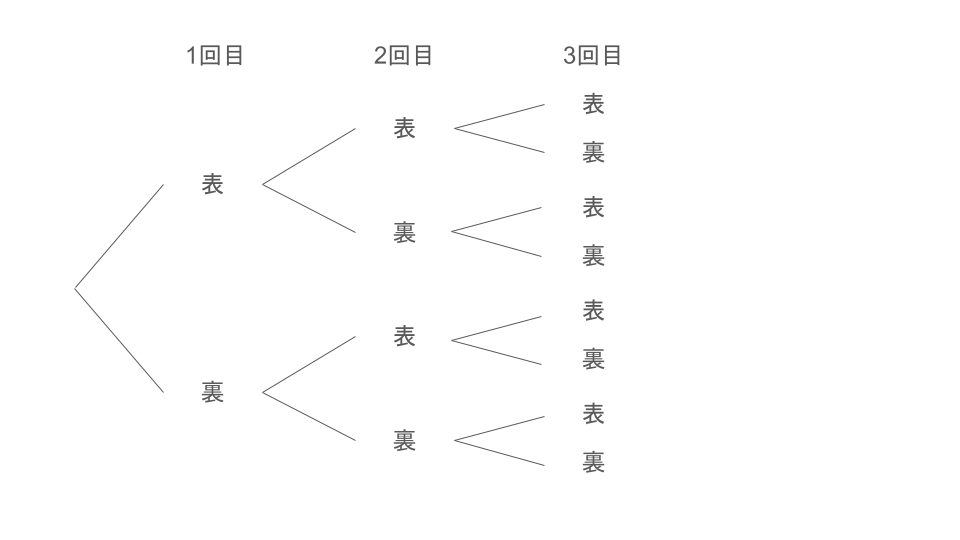
下のような図を樹形図とよぶ。
(コインを3回投げるとき、表裏の出方)
和の法則・積の法則
和の法則
2つの事象 \(A, B\) が同時には起こらないとする。\(A\) の起こり方が \(m\) 通り、\(B\) の起こり方が \(n\) 通りあるとき、\(A\) または\(B\) の起こり方は \(m + n\) 通りである。
積の法則
\(A\) の起こり方が \(m\) 通り、そのおのおのに対して \(B\) の起こり方が \(n\) 通りあるとき、\(A\) と \(B\) が両方起こる場合の数は \(mn\) 通りである。
補足
和の法則、積の法則は集合の要素の個数、樹形図が分かれば自然と分かるものであるため、理解できれば覚える必要はない。
階乗・順列
階乗
自然数 \(n\) において、
\[
n! = n(n \ – \ 1)(n \ – \ 2) \cdots 2 \cdot 1
\]
を \(n\) の階乗とよぶ。
順列
\(n \geq r \) をみたす自然数 \(n, r\) において、\(n\) 個の異なったものから \(r\) 個を選んで、順番をつけて並べる仕方の数を \({}_n P_{r}\)と書く。
最初に並べるものが \(n\) 通り、次に並べるものが \(n \ – \ 1\)、\(\cdots\)、最後に選ぶものが \(n \ – \ (r \ – \ 1)\) であるため、
\[\begin{align}
{}_n P_{r} &= n (n \ – \ 1)(n \ – \ 2) \cdots (n \ – \ r + 1) \\
&= \frac{n (n \ – \ 1)(n \ – \ 2) \cdots (n \ – \ r + 1)(n \ – \ r)(n \ – \ r \ – \ 1) \cdots 2 \cdot 1}{(n \ – \ r)(n \ – \ r \ – \ 1) \cdots 2 \cdot 1} \\
&= \frac{n!}{(n \ – \ r)!}
\end{align}\]
なお、\({}_n P_{r}\) の \(P\) は、順列を意味する英語 permutation の頭文字である。
組合せ
\(n \geq r \) をみたす自然数 \(n, r\) において、\(n\) 個の異なったものから \(r\) 個を選んで、順番をつけずに並べる仕方の数を \({}_n C_{r}\)と書き、このような計算を組み合わせ(combination) という。
\(a, b, c, d, e\) の5文字から3文字を選ぶときの選び方を考える。このとき、
\[
(a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a)
\]
は順番が異なるだけで同じものであり、順番を考慮しなければ1通りである。この議論は他の要素でも起きているので、\(a, b, c, d, e\) の5文字から3文字を選ぶときの選び方は
\[
\frac{{}_5 P_3}{3!} = \frac{5 \cdot 4 \cdot 3}{3 \cdot 2 \cdot 1} = 10 \text{通り}
\]
となる。すなわち、\({}_5 C_{3} = \frac{{}_5 P_3}{3!} = 10\) である。
この議論を一般化すると、
\[
{}_n C_{r} = \frac{{}_n P_r}{r!} = \frac{n!}{r! (n \ – \ r)!}
\]
が得られる。
練習問題
下記の練習問題の中で公式を紹介しておりますが、その導出はすべて上記の知識から導けるものです。公式として覚えることよりも、導出を理解し、考え方を学ぶほうが重要になります。最終手段としてすべての場合の数を数えるという方法はありますが、工夫して考えたり、計算をしたりすることで楽に求められるようにしましょう。
順列の基本
練習問題1
問題
次の値を求めよ。
(1) \({}_6 P_3\)
(2) \({}_4 P_4\)
(3) \({}_8 P_1\)
(4) \({}_{10} P_2\)
(5) \(6!\)
解答
(1) \({}_6 P_3 = 6 \cdot 5 \cdot 4 = 120\)
(2) \({}_4 P_4 = 4 \cdot 3 \cdot 2 \cdot 1 = 24\)
(3) \({}_8 P_1 = 8\)
(4) \({}_{10} P_2 = 10 \cdot 9 = 90\)
(5) \(6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\)
練習問題2
問題
次の問いに答えよ。
(1)8人の生徒から学級委員、保健委員、体育委員を1人ずつ選ぶときの選び方の総数を求めよ。
(2)4人の生徒がA, B, C, D, E, Fの6つの椅子のいずれかに座るときの場合の数を求めよ。
解答
(1)\({}_8 P_3 = 8 \cdot 7 \cdot 6 = 336\) 通り
(2)\({}_6 P_4 = 6 \cdot 5 \cdot 4 \cdot 3 = 360\) 通り
練習問題3
問題
男子4人と女子3人を1列に並べるとき、次の並び方は何通りあるか。
(1)少なくとも一方の端に女子が並ぶ
(2)男子と女子が交互に並ぶ
解答
(1)7人が1列に並ぶときの並び方は \(7! = 5040\) 通り。
両端がどちらも男子になる並び方は \({}_4 P_2 \cdot 5! = 1440\) 通り。
よって、求める場合の数は \(5040 – 1440 = 3600\) 通り。
(2)男子と女子が交互に並ぶとき、男子の並べる箇所は4通り、女子の並べる箇所は3通りであり、それらは重複していない。よって、求める場合の数は、\(4! \cdot 3! = 144\) 通り。
解説
(1)(男, 〇, 〇, 〇, 〇, 〇, 男)のように並べばよい。両端の男子の並び方は \({}_4 P_2^) 通りであり、その間の5か所は残りの5人が並ぶと考えればよい。
(2)(男, 女, 男, 女, 男, 女, 男)のように並ぶ。
重複順列
重複順列の公式
\(n, r\) を自然数とする。
異なる \(n\) 種類のものから、重複を許して \(r\) 個取り出して並べる順列の個数は \(n^r\) 個である。
練習問題4
問題
1, 2, 3, 4 の4つの数字から重複を許して作ることができる3桁の整数は何通りか。
解答
\(4^3 = 64\) 通り
解説
百の位、十の位、一の位すべて1、2、3、4 の4通りである。
同じものを含む順列
同じものを含む順列の公式
\(n\)を自然数とする。\(n\)個のもののうち、\(p\)個、\(q\)個、\(r\)個、\(\cdots\)が同じものであるとき、それら \(n\)個のものすべてを1列に並べる順列の総数は
\[\begin{align}
{}_n C_{p} \times {}_{n – p} C_{q} \times {}_{n – p – q} C_{r} \times \cdots &= \frac{{}_n P_{p}}{p!} \cdot \frac{{}_{n – p} P_{q}}{q!} \cdot \frac{{}_{n – p – q} P_{r}}{r!} \cdots \\
&= \frac{n!}{p! q! r! \cdots}
\end{align}\]
ただし、\(p + q + r + \cdots = n\) である。
練習問題
問題
白玉3個、赤玉2個、青玉1個の並べ方は何通りあるか。ただし、同じ色の玉は区別しないものとする。
解答
\(\frac{6!}{3! 2! 1!} = 5! = 120\) 通り。
解説
同じものを含む順列の公式を用いた。\(C\)を用いるのであれば、
(〇, 〇, 〇, 〇, 〇, 〇)の6か所から白玉が入る箇所を3つ、白玉が入っていない残りの3つから赤玉が入る箇所を2つ、最後の1か所を青玉にすればよいので、
\[
{}_6 C_{3} \times {}_3 C_{2} \times {}_1 C_{1} = \frac{6 \cdot 5 \cdot 4}{3!} \cdot \frac{3 \cdot 2}{2!} \cdot \frac{1}{1} = 120
\]
より120通りとも求められる。
円順列・じゅず順列
円順列の公式
異なる \(n\) 個のものを円形に並べる方法の総数は
\[
(n \ – \ 1)! \text{通り}
\]
導出
\(n = 5\) の場合で考える。
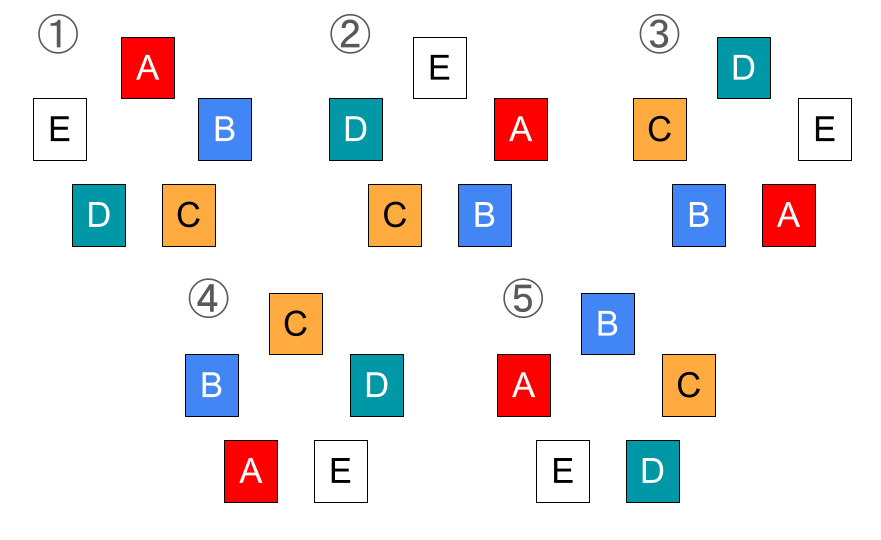
異なる5つのものを一列に並べる方法の総数は \(5!\) 通り。このとき、一列に並べる場合は別のものとして扱われるが、円形に並べた場合に同じものとして扱われるものを考える。
- (A, B, C, D, E)
- (B, C, D, E, A)
- (C, D, E, A, B)
- (D, E, A, B, C)
- (E, A, B, C, D)
すべての要素に対して、同じものとして扱われるものが \(5\) つあるため、異なる \(5\) 個のものを円形に並べる方法の総数は
\[
\frac{5!}{5} = 4!
\]
となる。同様の議論を一般の \(n\) にもできるため、異なる \(n\) 個のものを円形に並べる方法の総数は
\[
\frac{n!}{n} = (n \ – \ 1)!
\]
が得られる。
じゅず順列の公式
異なる \(n\) 個のものをじゅず順列で並べるとき、並べ方の総数は
\[
\frac{(n \ – \ 1)!}{2} \text{通り}
\]
導出
じゅず順列は、円順列のように回転させて一致するものに加え、ひっくり返したときに一致するものも1通りとして数える順列です。
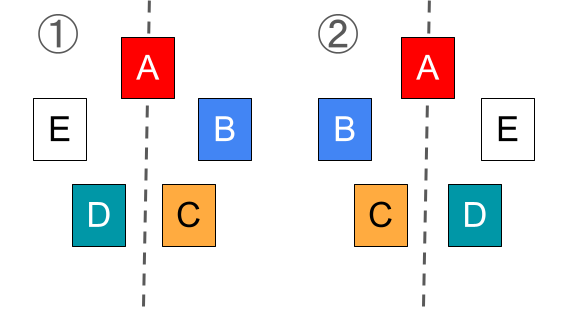
円順列の場合から、さらにひっくり返したものも同じものとして考えます。そのため、異なる \(n\) 個のものを円順列で並べるときの並べ方の総数を半分にすればよいため、
\[
\frac{(n \ – \ 1)!}{2}
\]
が得られる。
練習問題1
問題
大人3人と子供3人が円形のテーブルに座るとき、大人と子供が交互に並ぶ並び方の総数を求めよ。
解答
まず大人を円形に並べる並べ方は\((3 \ – \ 1)! = 2! = 2\) 通り。この大人の間に子供を入れればよいため、\(3! = 6\) 通り。したがって、
\[
2 \times 6 = 12 (\text{通り})
\]
練習問題2
問題
赤、白、青、黄、緑の5つの玉でじゅずをつくるとき、作り方は何通りあるか。
解答
\[
\frac{(5 \ – \ 1)!}{2} = \frac{4!}{2} = 12 (\text{通り})
\]
最短経路の総数
例題
問題
下の図において、点Pから点Qまでの最短経路は何通りあるか。
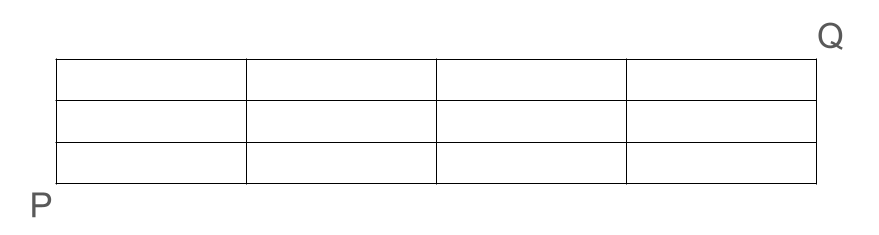
解答
\[
\frac{7!}{3! 4!} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35 (\text{通り})
\]
解説
右に4回、上に3回移動すればよい。そのため、最短経路の総数は右4つ、上3つの並べ方に一致する。上記の解答は同じものを含む順列の考え方を用いている。7回の移動のうち、上に移動する3回を選ぶと考えると、\({}_7 C_3 = 35\) と求めることも可能である。
練習問題
問題
下の図において、点Pから点Aを通って点Qまで移動するときの最短経路は何通りあるか。
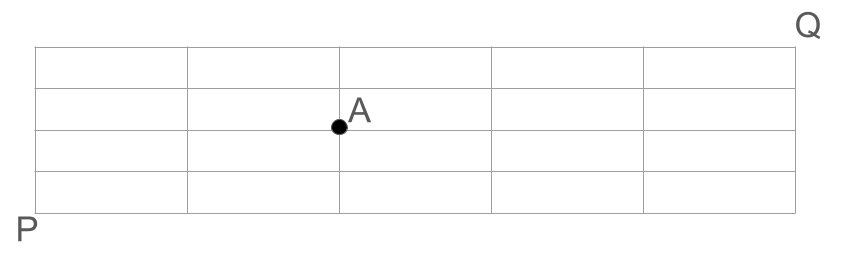
解答
点Pから点Aまでの最短経路は \(\frac{4!}{2!2!} = 6\) 通り。点Aから点Qまでの最短経路は \(\frac{5!}{3!2!} = 10\) 通り。したがって、点Pから点Aを通って点Qまで移動するときの最短経路は \(6 \times 10 = 60\) 通り。
重複組合せ
重複組合せの公式
\(n\) 種類のものから重複を許して \(r\) 個選ぶ場合の数は \({}_{n + r – 1} C_r\) 通り。
\({}_n H_r = {}_{n + r – 1} C_r\) と書くこともある。
この公式の導出は例題の解説を一般化すればよい。
例題
問題
3 種類の果物,りんご,なし,みかんから重複を許して 5 個選んで買う組合せの総数は何通りか。
解答
\({}_{3 + 5 – 1} C_5 = {}_7 C_5 = 21\) 通り
解説
5つの〇と2つの区切り線|を用いて考える。
(りんごの個数)|(なしの個数)|(みかんの個数)とする。
例えば、
〇|〇|〇〇〇:りんご1個、なし1個、みかん3個
〇〇〇〇〇||:りんご5個、なし0個、みかん0個
といった具合である。
この5つの〇と2つの区切り線の並べ方と求める組合せの総数は一致するので、\({}_7 C_5 = {}_7 C_2 = 21\) 通り。
練習問題
問題
1から6までの6つの数字から重複を許して4個を選ぶとき、選び方は何通りあるか。
解答
\({}_{6 + 4 – 1} C_4 = {}_9 C_4 = 9 \times 7 \times 2 = 126\) 通り
解説
4つの〇と5つの区切り線で対応づける。
例えば、
|〇|〇||〇〇|:2が1つ、3が1つ、5が2つ
〇〇|||||〇〇:1が2つ、6が2つ
と考える。すると、4つの〇と5つの区切り線の並べ方と求める組合せの総数は一致するので、\({}_9 C_4 = 126\) 通り。