初めに
数学Bの確率分布と統計的な推測では、まず、確率変数と確率分布を学びます。本記事では、確率変数と確率分布を定義し、確率変数の期待値、分散、標準偏差が求められるようにします。
確率変数と確率分布
定義(確率変数、確率分布)
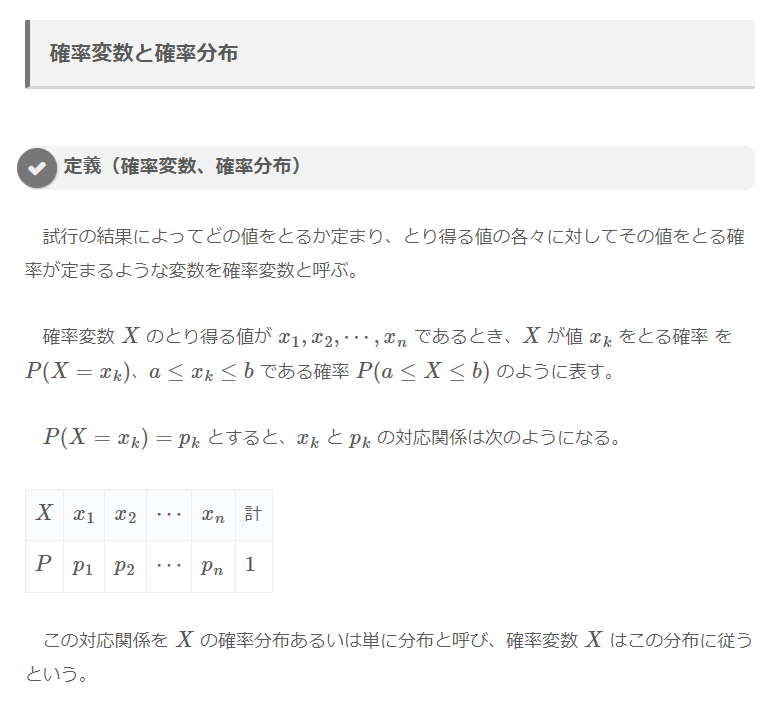
試行の結果によってどの値をとるか定まり、とり得る値の各々に対してその値をとる確率が定まるような変数を確率変数と呼ぶ。
確率変数 \(X\) のとり得る値が \(x_1, x_2, \cdots, x_n\) であるとき、\(X\) が値 \(x_k\) をとる確率 を \(P(X = x_k)\)、\(a \leq x_k \leq b\) である確率 \(P(a \leq X \leq b)\) のように表す。
\(P(X = x_k) = p_k\) とすると、\(x_k\) と \(p_k\) の対応関係は次のようになる。
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | \(x_n\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | \(1\) |
この対応関係を \(X\) の確率分布あるいは単に分布と呼び、確率変数 \(X\) はこの分布に従うという。
確率分布の性質
確率変数 \(X\) の確率分布が以下の表であるとする。
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | \(x_n\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | \(1\) |
このとき、
\[\begin{align}
& p_k \geq 0 \ (k = 1, 2, \cdots, n) \notag \\
& \sum_{k = 1}^n p_k = 1 \notag
\end{align}\]
が成り立つ.
期待値と分散
定義(確率変数の期待値、分散、標準偏差)
確率変数 \(X\) の確率分布が以下の表であるとする。
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | \(x_n\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | \(1\) |
このとき、\(X\) の期待値 \(E(X)\) または \(m\) または \(\mu\)、分散 \(V(X)\)、標準偏差 \(\sigma(X)\) を次で定義する。
\[\begin{align}
E(X) &= \sum_{k = 1}^n x_k p_k (= m = \mu) \notag \\
V(X) &= E((X \ – \ m)^2) = \sum_{k = 1}^n (x_k \ – \ m)^2 p_k \notag \\
\sigma(X) &= \sqrt{V(X)} \notag
\end{align}\]
定数の期待値、分散
定数 \(a\) において、次が成り立つ。
\[\begin{align}
E(a) &= a \notag \\
V(a) &= 0 \notag
\end{align}\]
証明
\(a\) は定数であるので、次の表に従う確率変数 \(A\) を考えればよい。
| \(A\) | \(a\) | 計 |
| \(P\) | \(1\) | \(1\) |
すると、
\[\begin{align}
E(a) &= a \times 1 = a \notag
V(a) &= E((a – a)^2) = E(0) = 0 \notag
\end{align}\]
となる。
分散の公式
確率変数 \(X\) において、\(E(X)\) を \(X\) の期待値、\(E(X^2)\) を \(X^2\) の期待値、\(V(X)\) を \(X\) の分散とする。このとき、次が成り立つ。
\[
V(X) = E(X^2) \ – \ \{E(X)\}^2
\]
証明
\[\begin{align}
V(X) &= E((X \ – \ m)^2) \notag \\
&= E(X^2 \ – \ 2mX + m^2) \notag \\
&= E(X^2) \ – \ 2m E(X) + E(m^2) \notag \\
&= E(X^2) \ – \ 2m \times m + m^2 \notag \\
&= E(X^2) \ – \ m^2 \notag
\end{align}\]
\(m = E(X)\) より示された。
補足
証明には、同時分布と呼ばれる二つの確率変数に関する和の期待値の性質 \(E(a X + b Y) = a E(X) + b E(Y)\) を用いている。\(\sum\)を用いて計算すれば変数の変換を使わずに証明ができる。
確率変数の変換
\(a, b\) を実数、\(X\) を次の表に従う確率分布であるとする。
| \(X\) | \(x_1\) | \(x_2\) | \(\cdots\) | \(x_n\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | \(1\) |
このとき、\(Y = aX + b\) は確率変数となり、\(Y\) は \(y_k = a x_k + b \ (k = 1, 2, \cdots, n)\) をとる。また、下の表に従い、次の式が成り立つ。
| \(Y\) | \(y_1\) | \(y_2\) | \(\cdots\) | \(y_n\) | 計 |
| \(P\) | \(p_1\) | \(p_2\) | \(\cdots\) | \(p_n\) | \(1\) |
\[\begin{align}
E(Y) &= E(aX + b) = a E(X) + b \notag \\
V(Y) &= V(aX + b) = a^2 V(X) \notag \\
\sigma(Y) &= \sigma(aX + b) = |a| \sigma(X)
\end{align}\]
証明
\(E(Y) = E(aX + b) = a E(X) + b\) は明らか。
\[\begin{align}
V(Y) &= V(aX + b) \notag \\
&= E((aX + b)^2) \ – \ (a E(X) + b)^2 \notag \\
&= E(a^2 X^2 + 2abX + b^2) \ – \ (a^2 \{E(X)\}^2+ 2ab E(X) + b^2) \notag \\
&= E(a^2 X^2) + 2ab E(X) + E(b^2) \ – \ (a^2 \{E(X)\}^2+ 2ab E(X) + b^2) \notag \\
&= a^2 E(X^2) \ – \ a^2 \{E(X)\} \notag \\
&= a^2 V(X) \notag
\end{align}\]
\(\sigma(Y) = \sqrt{V(Y)} = \sqrt{a^2 V(X)} = |a| \sigma(X)\) より標準偏差も示せた。
補足
分散の公式の証明と同様に \(E(a X + b Y) = a E(X) + b E(Y)\) を用いている。これも \(\sum\) に直せばこの性質を使わずに証明できる。
練習問題
練習問題1
問題
さいころを1回投げる試行をするとき、サイコロの出た目を \(X\) とする。このとき、\(X\)は次の分布に従う。
| \(X\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | 計 |
| \(P\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(1\) |
(1) \(X\) の期待値、分散、標準偏差を求めよ。
(2) 確率変数 \(Y = 3X + 2\) の期待値、分散、標準偏差を求めよ。
解答
(1)
\[\begin{align}
E(X) &= \sum_{k = 1}^6 k \times \frac{1}{6} = \frac{1}{6} \times \frac{1}{2} \times 6 \times 7 = \frac{7}{2} \notag \\
V(X) &= E(X^2) – \{E(X)\}^2 \notag \\
&= \sum_{k = 1}^6 k^2 \times \frac{1}{6} – (\frac{7}{2})^2 \notag \\
&= \frac{1}{6} \times \frac{1}{6} \times 6 \times 7 \times 13 – \frac{49}{4} \notag \\
&= \frac{91}{6} – \frac{49}{4} \notag \\
&= \frac{35}{12} \notag \\
\sigma (X) &= \sqrt{V(X)} = \sqrt{\frac{35}{12}} = \frac{\sqrt{105}}{6} \notag
\end{align}
\]
(2)
\[\begin{align}
E(Y) &= 3 E(X) + 2 = 3 \times \frac{7}{2} + 2 = \frac{25}{2} \notag \\
V(Y) &= 3^2 V(X) = 9 \times \frac{35}{12} = \frac{105}{4} \notag \\
\sigma (Y) &= |3| \sigma (X) = 3 \times \frac{\sqrt{105}}{6} = \frac{\sqrt{105}}{2} \notag
\end{align}\]
参考