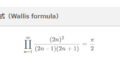初めに
\(\displaystyle{\int_{0}^{\frac{\pi}{2}} \sin^n x dx, \int_{0}^{\frac{\pi}{2}} \cos^n x dx}\) をウォリス積分といいます。本記事はウォリスの公式にも使われるウォリス積分を紹介します。
ウォリス積分
ウォリス積分
\[\begin{align}
& \int_{0}^{\frac{\pi}{2}} \sin^n x dx = \int_{0}^{\frac{\pi}{2}} \cos^n x dx =
\left\{\begin{array}{ll}
\frac{(n \ – \ 1)!!}{n!!} \ (n : \text{奇数}) \\
\frac{(n \ – \ 1)!!}{n!!} \frac{\pi}{2} \ (n : \text{偶数}) \\
\end{array}\right.
\end{align}\]
ここで \(n!!\) は二重階乗であり次で与えられる。
\[\begin{align}
n!! = n(n \ – \ 2) \cdots = \left\{\begin{array}{ll}
n (n \ – \ 2) \cdots 3 \cdot 1 \ (n : \text{奇数}) \\
n (n \ – \ 2) \cdots 4 \cdot 2 \ (n : \text{偶数}) \\
\end{array}\right.
\end{align}\]
証明
\(I_n = \int_{0}^{\frac{\pi}{2}} \sin^n x dx \) とおく。\(I_n\) を部分積分すると
\[\begin{align}
I_n &= \int_{0}^{\frac{\pi}{2}} \sin x \sin^{n \ – \ 1} x dx \notag \\
&= \left[- \cos x \sin^{n – 1} x \right]_0^{\frac{\pi}{2}} + (n \ – \ 1) \int_{0}^{\frac{\pi}{2}} \cos^2 x \sin^{n \ – \ 2} x dx \notag \\
&= (n \ – \ 1) \int_{0}^{\frac{\pi}{2}} (1 \ – \ \sin^2 x) \sin^{n \ – \ 2} x dx \notag \\
&= (n \ – \ 1) \int_{0}^{\frac{\pi}{2}} \sin^{n \ – \ 2} x dx \ – \ (n \ – \ 1) \int_{0}^{\frac{\pi}{2}} \sin^n x dx \notag \\
&= (n \ – \ 1) I_{n \ – \ 2} + (n \ – \ 1) I_n
\end{align}\]
したがって、\(\displaystyle{I_n = \frac{n \ – \ 1}{n} I_{n \ – \ 2}}\) という漸化式が成り立つ。
\(n\) が奇数のとき
\[\begin{align}
I_n &= \frac{n \ – \ 1}{n} I_{n \ – \ 2} \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} I_{n \ – \ 4} \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{4}{5} \frac{2}{3} I_1 \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{4}{5} \frac{2}{3} \int_{0}^{\frac{\pi}{2}} \sin x dx \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{4}{5} \frac{2}{3} \notag \\
&= \frac{(n \ – \ 1)!!}{n!!} \notag
\end{align}\]
\(n\) が偶数のとき
\[\begin{align}
I_n &= \frac{n \ – \ 1}{n} I_{n \ – \ 2} \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} I_{n \ – \ 4} \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{3}{4} \frac{1}{2} I_0 \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{3}{4} \frac{1}{2} \int_{0}^{\frac{\pi}{2}} \sin^0 x dx \notag \\
&= \frac{n \ – \ 1}{n} \frac{n \ – \ 3}{n \ – \ 2} \cdots \frac{3}{4} \frac{1}{2} \frac{\pi}{2} \notag \\
&= \frac{(n \ – \ 1)!!}{n!!} \frac{\pi}{2} \notag
\end{align}\]
以上で \(\displaystyle{\int_{0}^{\frac{\pi}{2}} \sin^n x dx}\) が求まった。
次に \(\displaystyle{\int_{0}^{\frac{\pi}{2}} \sin^n x dx = \int_{0}^{\frac{\pi}{2}} \cos^n x dx}\) を示す。
\(\displaystyle{\int_{0}^{\frac{\pi}{2}} \cos^n x dx}\) を \(t = \frac{\pi}{2} \ – \ x\) で置換をする。\(dt = – dx\) であり、
| \(x\) | \(0 \rightarrow \frac{\pi}{2}\) |
| \(t\) | \(\frac{\pi}{2} \rightarrow 0\) |
であるため、
\[\begin{align}
\int_{0}^{\frac{\pi}{2}} \cos^n x dx &= \int_{\frac{\pi}{2}}^0 \cos^n \left(\frac{\pi}{2} \ – \ t \right) (- dt) \notag \\
&= \int_{0}^{\frac{\pi}{2}} \cos^n \left(\frac{\pi}{2} \ – \ t \right) dt \notag \\
&= \int_{0}^{\frac{\pi}{2}} \sin^n t dt \notag
\end{align}\]
が成り立つ。以上より題意は示せた。
補足
\(n\) 乗だけでなく、積分可能な関数 \(f\) において、
\[
\int_0^{\frac{\pi}{2}} f(\cos x) dx = \int_0^{\frac{\pi}{2}} f(\sin x) dx
\]
が成り立つ。これは King Property
\[
\int_a^b f(x) dx = \int_a^b f(a + b \ – \ x) dx
\]
の一例であることでも知られている。