初めに
統計学では、変数を性質に応じて、4つの尺度にわけて考えることがあります。本記事では、それらの尺度とその見分け方についてまとめます。
変数の尺度
概要
統計学では、変数を次の4つの尺度にわけて考えることがあります。
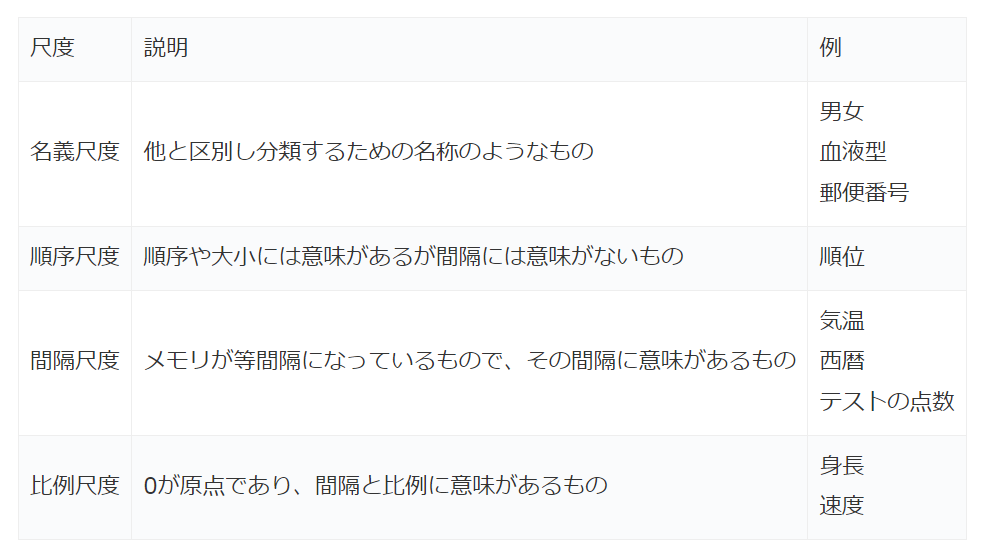
| 尺度 | 説明 | 例 |
| 名義尺度 | 他と区別し分類するための名称のようなもの | 男女 血液型 郵便番号 |
| 順序尺度 | 順序や大小には意味があるが間隔には意味がないもの | 順位 |
| 間隔尺度 | メモリが等間隔になっているもので、その間隔に意味があるもの | 気温 西暦 テストの点数 |
| 比例尺度 | 0が原点であり、間隔と比例に意味があるもの | 身長 速度 |
質的データ・量的データ
| 分類 | 説明 | 該当する尺度 |
| 質的データ | 数値や量で測ることのできないデータ | 名義尺度 順序尺度 |
| 量的データ | 数値や量で測ることのできるデータ | 間隔尺度 比例尺度 |
質的データは質的変数やカテゴリカルデータ、カテゴリーデータとも呼ばれます。
量的データは量的変数や数量データとも呼ばれます。
名義尺度
他と区別し分類するための尺度が名義尺度です。
- 性別（男：0、女：1）
- 血液型（A：0、B：1、AB：2、O：3）
順序尺度
順序や大小には意味があるが間隔には意味がないものが順序尺度です。
- 順位（1位、2位、3位）
- 級（1級、2級、3級）
- モース硬度（滑石：1、石膏：2、\(\cdots\)、ダイヤモンド：10）
間隔尺度
メモリが等間隔になっているもので、その間隔に意味があるものが間隔尺度です。
- 気温
- 西暦
- テストの点数
比例尺度
0が原点であり、間隔と比例に意味があるものが比例尺度です。
- 身長
- 速度
間隔尺度と比例尺度の見分け方
間隔尺度と比例尺度は \(0\) に着目すると見分けることができます。
比例尺度の場合 \(0\) はないことを表します。身長 \(0\) cm は存在せず、速度 \(0\) m/s も動いていません。
間隔尺度の場合の \(0\) はないわけではありません。気温 \(0\)℃も気温がないわけではなく、西暦 \(0\) 年も西暦がないわけではありません。
参考
1-4. 変数の尺度 | 統計学の時間 | 統計WEB
統計学の「1-4. 変数の尺度」についてのページです。統計WEBの「統計学の時間」では、統計学の基礎から応用までを丁寧に解説しています。大学で学ぶ統計学の基礎レベルである統計検定2級の範囲をほぼ全てカバーする内容となっています。
bellcurve.jp
モース硬度 - Wikipedia
ja.wikipedia.org
