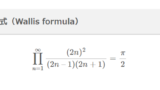スターリングの公式（Stirling’s formula）

初めに

本記事では、スターリングの公式を示す。ド・モアブル-ラプラスの定理（二項分布がサンプル数が十分大きいとき正規分布に近似できる）の証明に使われる公式です。

スターリングの公式（Stirling’s formula）

$$n!\fallingdotseq \sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n$$
ここで $f(n)\fallingdotseq g(n)$ は $f(n)$ と $g(n)$ が漸近的に等しいこと、すなわち ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\frac{f(x)}{g(x)}=1}$ を表す。

証明

証明には次の2つを使用します。

• ウォリスの公式
• 下に有界な単調減少数列は収束する

ウォリスの公式

$$\begin{array}{r}\prod _{n=1}^{\mathrm{\infty }}\frac{(2n{)}^2}{(2n–1)(2n+1)}=\frac{\pi }{2}\end{array}$$​

証明など詳細は下の記事をご覧ください。

ウォリスの公式（Wallis formula）

初めに ウォリスの公式（Wallis formula） \​ 証明 ウォリス積分 ウォリス積分を用いて証明する。 \ここで $n!!$ は二重階乗であり次で与えられる。\ 証明など詳細はリンク先をご覧ください。 証明 \(\displa...

ds-path.com

2024.06.01

下に有界な単調減少数列は収束する

$\{a_n\}$ を広義単調減少、かつ下に有界な実数の数列とする。このとき、数列 $\{a_n\}$ は収束する。

証明など詳細は下の記事をご覧ください。上に有界な単調増加列は収束することと合わせて証明しています。

https://ds-path.com/math/university-math/convergence_of_monotone_bounded_sequences/(

ds-path.com

新しいタブで開く)

証明

${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\frac{n!e^n}{\sqrt{2\pi n}{n}^n}=1}$ を示せばよい。

収束することの証明

まず、${\displaystyle a_n=\frac{n!e^n}{\sqrt{2\pi n}{n}^n}}$ が $n\to \mathrm{\infty }$ で収束することを示す。

任意の自然数 $n$ において、$a_n>0$ であるので下に有界であることは明らか。また、
$$\begin{array}{rl}\log \frac{a_n}{a_{n+1}}& =\log \frac{n!e^n(n+1{)}^{n+1}\sqrt{n+1}}{n^n\sqrt{n}(n+1)!e^{n+1}}\\ & =\log \frac{n+1}{(n+1)e}{(1+\frac{1}{n})}^{n+\frac{1}{2}}\\ & =(n+\frac{1}{2})\log (1+\frac{1}{n})–1\end{array}$$
これを $n$ で微分すると
$$\begin{array}{rl}\frac{d}{dn}(\log \frac{a_n}{a_{n+1}})& =\log (1+\frac{1}{n})+(n+\frac{1}{2})\cdot \frac{-\frac{1}{n^2}}{1+\frac{1}{n}}\\ & =\log (1+\frac{1}{n})–\frac{n+\frac{1}{2}}{n^2}\\ \frac{d^2}{d{n}^2}(\log \frac{a_n}{a_{n+1}})& =–\frac{-\frac{1}{n^2}}{1+\frac{1}{n}}–\frac{n(n+1)–(n+\frac{1}{2})(2n+1)}{n^2(n+1{)}^2}\\ & =\frac{1}{2n^2(n+1{)}^2}\end{array}$$
となる。$n\ge 1$ において、${\displaystyle \frac{d^2}{d{n}^2}(\log \frac{a_n}{a_{n+1}})>0}$ より $n\ge 1$ で ${\displaystyle \frac{d}{dn}(\log \frac{a_n}{a_{n+1}})}$ は単調増加である。また、${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\frac{d}{dn}(\log \frac{a_n}{a_{n+1}})=0}$ である。したがって、$n\ge 1$ において $\frac{d}{dn}(\log \frac{a_n}{a_{n+1}})<0$であり、${\displaystyle \log \frac{a_n}{a_{n+1}}}$ は単調減少である。また、

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\log \frac{a_n}{a_{n+1}}& =\underset{n\to \mathrm{\infty }}{lim}((n+\frac{1}{2})\log (1+\frac{1}{n})–1)\\ & =\underset{n\to \mathrm{\infty }}{lim}(\log {(1+\frac{1}{n})}^n+\frac{1}{2}\log (1+\frac{1}{n})–1)\\ & =1+0–1\\ & =0\end{array}$$
より $\log \frac{a_n}{a_{n+1}}>0$ となる。よって、$\{a_n\}$ は単調減少である。以上より数列 $\{a_n\}$ は広義単調減少、かつ下に有界な数列であるため、収束する。

収束先が正の数であることの証明

次に ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\frac{n!e^n}{\sqrt{2\pi n}{n}^n}=A}$ としたとき、$A>0$ であることを示す。

まず、$n\ge 1$ で次の不等式が成り立つことを示す。
$$\log \frac{a_n}{a_{n+1}}=(n+\frac{1}{2})\log (1+\frac{1}{n})–1<\frac{1}{4n(n+1)}$$
これを示すには、
$$h(n):=\frac{1}{4n(n+1)}–((n+\frac{1}{2})\log (1+\frac{1}{n})–1)>0$$
を示せばよい。

${\displaystyle g(n)=\frac{1}{4n(n+1)}}$ とおくと
$$\begin{array}{rl}\frac{dg}{dn}(n)& =–\frac{1}{4}\cdot \frac{2n+1}{n^2(n+1{)}^2}\\ \frac{d^{2}g}{d{n}^2}(n)& =–\frac{1}{4}\cdot \frac{2n^2(n+1{)}^2–(2n+1)(4n^3+6n^2+2n)}{n^4(n+1{)}^4}\\ & =\frac{1}{4}\cdot \frac{6n^3+12n^2+8n+2}{n^3(n+1{)}^4}\\ & =\frac{1}{4}\cdot \frac{(n+1)(6n^2+6n+2)}{n^3(n+1{)}^4}\\ & =\frac{1}{4}\cdot \frac{6n^2+6n+2}{n^3(n+1{)}^3}\end{array}$$

となる。よって、
$$\begin{array}{rl}\frac{d^{2}h}{d{n}^2}(n)& =\frac{d^{2}g}{d{n}^2}(n)–\frac{d^2}{d{n}^2}(\log \frac{a_n}{a_{n+1}})\\ & =\frac{1}{4}\cdot \frac{6n^2+6n+2}{n^3(n+1{)}^3}–\frac{1}{2n^2(n+1{)}^2}\\ & =\frac{2n^2+2n+1}{2n^3(n+1{)}^3}\\ & =\frac{2(n+\frac{1}{2}{)}^2+\frac{1}{2}}{2n^3(n+1{)}^3}>0\end{array}$$
であり、${\displaystyle \frac{dh}{dn}(n)}$ は単調増加である。また、
$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\frac{dh}{dn}(n)& =\underset{n\to \mathrm{\infty }}{lim}(\frac{dg}{dn}(n)–\frac{d}{dn}(\log \frac{a_n}{a_{n+1}}))\\ & =\underset{n\to \mathrm{\infty }}{lim}(-\frac{1}{4}\cdot \frac{2n+1}{n^2(n+1{)}^2}–\log (1+\frac{1}{n})–\frac{n+\frac{1}{2}}{n^2})\\ & =0\end{array}$$
より${\displaystyle \frac{dh}{dn}(n)<0}$ であるため、$h(x)$ は単調減少である。上記より ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\log \frac{a_n}{a_{n+1}}=0}$ であったことに注意すると
$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}h(n)& =\underset{n\to \mathrm{\infty }}{lim}(\frac{1}{4n(n+1)}–\log \frac{a_n}{a_{n+1}})\\ & =0–0\\ & =0\end{array}$$
となる。よって、$h(n)>0$ が成り立ち、
$$(n+\frac{1}{2})\log (1+\frac{1}{n})–1<\frac{1}{4n(n+1)}$$
が示せた。

いま、
$$\log \frac{a_n}{a_{n+1}}<\frac{1}{4n(n+1)}=\frac{1}{4}\left(\frac{1}{n}–\frac{1}{n+1}\right)$$
より
$$\begin{array}{rl}\log \frac{a_1}{a_n}& =\log (\frac{a_1}{a_2}\cdot \frac{a_2}{a_3}\cdots \frac{a_{n–1}}{a_n})\\ & =\sum _{i=1}^{n–1}\log \frac{a_i}{a_{i+1}}\\ & <\sum _{i=1}^{n–1}\frac{1}{4}\left(\frac{1}{i}–\frac{1}{i+1}\right)\\ & =\frac{1}{4}(\left(1–\frac{1}{2}\right)+\left(\frac{1}{2}–\frac{1}{3}\right)+\cdots +\left(\frac{1}{n–1}–\frac{1}{n}\right))\\ & =\frac{1}{4}(1–\frac{1}{n})\\ & <\frac{1}{4}\end{array}$$
となる。$a_1=\frac{e}{\sqrt{2\pi }}$ より
$$\begin{array}{rl}\log \frac{a_1}{a_n}<\frac{1}{4}& \iff \log a_1–\log a_n<\frac{1}{4}\\ & \iff \log \frac{e}{\sqrt{2\pi }}–\log a_n<\frac{1}{4}\\ & \iff \log a_n>\frac{3}{4}+\log \frac{1}{\sqrt{2\pi }}\\ & \iff \log a_n>\log \frac{e^{\frac{3}{4}}}{\sqrt{2\pi }}\\ & \iff a_n>\frac{e^{\frac{3}{4}}}{\sqrt{2\pi }}\end{array}$$
である。したがって、任意の自然数 $n$ において、$a_n>0$ がいえた。

収束先が1であることの証明

ウォリスの公式

$$\begin{array}{r}\prod _{n=1}^{\mathrm{\infty }}\frac{(2n{)}^2}{(2n–1)(2n+1)}=\frac{\pi }{2}\end{array}$$​

を用いて示す。

ウォリスの公式の左辺を変形する。
$$\begin{array}{rl}\prod _{n=1}^{\mathrm{\infty }}\frac{(2n{)}^2}{(2n–1)(2n+1)}& =\frac{2^2}{1\times 3}\cdot \frac{4^2}{3\times 5}\cdots \\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{\{(2n)!!{\}}^2}{(2n–1)!!(2n+1)!!}\end{array}$$
となる。

$$\begin{array}{rl}\frac{1}{(2n–1)!!}& =\frac{1}{1\cdot 3\cdot 5\cdots (2n–1)}\\ & =\frac{2\cdot 4\cdot 6\cdots 2n}{(2n)!}\\ & =\frac{2^{n}n!}{(2n)!}\\ \frac{1}{(2n+1)!!}& =\frac{1}{1\cdot 3\cdot 5\cdots (2n+1)}\\ & =\frac{2\cdot 4\cdot 6\cdots 2n}{(2n)!(2n+1)}\\ & =\frac{2^{n}n!}{(2n)!(2n+1)}\end{array}$$
より
$$\begin{array}{rl}\prod _{n=1}^{\mathrm{\infty }}\frac{(2n{)}^2}{(2n–1)(2n+1)}& =\underset{n\to \mathrm{\infty }}{lim}\frac{\{(2n)!!{\}}^2(2^{n}n!{)}^2)}{\{(2n)!{\}}^2(2n+1)}\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{2^{4n}(n!{)}^4)}{\{(2n)!{\}}^2(2n+1)}\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{2^{4n}}{2n+1}{\left(\frac{n!e^n}{\sqrt{2\pi n}{n}^n}\right)}^4{\left(\frac{(2n{)}^{2n}\sqrt{2\pi \cdot 2n}}{(2n)!e^{2n}}\right)}^2\frac{\pi n}{2^{4n}}\end{array}$$

と式変形できる。よって、
$$\begin{array}{r}\frac{A^4}{A^2}\underset{n\to \mathrm{\infty }}{lim}\frac{\pi n}{2n+1}=\frac{\pi }{2}\end{array}$$
より ${\displaystyle \frac{\pi A^2}{2}=\frac{\pi }{2}}$ となる。$A>0$ より $A=1$ が示せる。