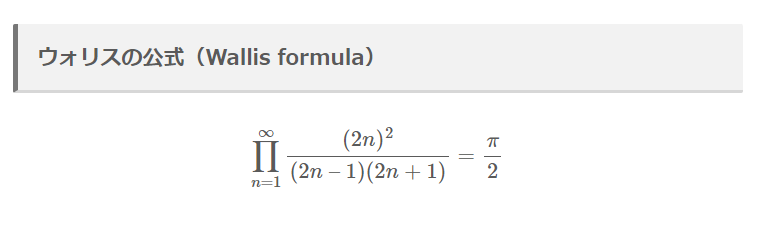初めに
ウォリスの公式(Wallis formula)
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} = \frac{\pi}{2}
\end{align}\]
証明
ウォリス積分
ウォリス積分を用いて証明する。
\[\begin{align}
& \int_{0}^{\frac{\pi}{2}} \sin^n x dx = \int_{0}^{\frac{\pi}{2}} \cos^n x dx =
\left\{\begin{array}{ll}
\frac{(n \ – \ 1)!!}{n!!} \ (n : \text{奇数}) \\
\frac{(n \ – \ 1)!!}{n!!} \frac{\pi}{2} \ (n : \text{偶数}) \\
\end{array}\right.
\end{align}\]
ここで \(n!!\) は二重階乗であり次で与えられる。
\[\begin{align}
n!! = n(n \ – \ 2) \cdots = \left\{\begin{array}{ll}
n (n \ – \ 2) \cdots 3 \cdot 1 \ (n : \text{奇数}) \\
n (n \ – \ 2) \cdots 4 \cdot 2 \ (n : \text{偶数}) \\
\end{array}\right.
\end{align}\]
証明など詳細はリンク先をご覧ください。

証明
\(\displaystyle{I_n = \int_{0}^{\frac{\pi}{2}} \sin^n x dx}\) とおく。\(0 \leq x \leq \frac{\pi}{2}\) の範囲では \(0 < \sin x < 1\) である。よって、\(I_{2n + 2} < I_{2n + 1} < I_{2n}\) である。
\[\begin{align}
I_{2n} &= \frac{(2n \ – \ 1)!!}{2n!!} \frac{\pi}{2} \notag \\
I_{2n + 1} &= \frac{(2n)!!}{(2n + 1)!!} \notag \\
I_{2n + 2} &= \frac{(2n + 1)!!}{(2n + 2)!!} \frac{\pi}{2} \notag \\
\end{align}\]
であるため、
\[
\frac{(2n + 1)!!}{(2n + 2)!!} \frac{\pi}{2} < \frac{(2n)!!}{(2n + 1)!!} < \frac{(2n \ – \ 1)!!}{2n!!} \frac{\pi}{2}
\]
各辺に \(\frac{(2n)!!}{(2n \ – \ 1)!!}\) をかけると
\[
\frac{2n + 1}{2n + 2} \cdot \frac{\pi}{2} < \frac{\{(2n)!! \}^2}{(2n \ – \ 1)!!(2n + 1)!!} < \frac{\pi}{2}
\]
\(n \rightarrow \infty\) とすると \(\frac{2n + 1}{2n + 2} \cdot \frac{\pi}{2} \rightarrow \frac{\pi}{2}\) であるため、はさみうちの原理より
\[
\lim_{n \rightarrow \infty} \frac{\{(2n)!! \}^2}{(2n \ – \ 1)!!(2n + 1)!!} = \frac{\pi}{2}
\]
が成り立つ。
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} &= \frac{2^2}{1 \times 3} \cdot \frac{4^2}{3 \times 5} \cdot \frac{6^2}{5 \times 7} \cdots \notag \\
&= \lim_{n \rightarrow \infty} \frac{\{(2n)!! \}^2}{(2n \ – \ 1)!!(2n + 1)!!} \notag \\
&= \frac{\pi}{2} \notag
\end{align}\]
より示された。
スターリングの公式
ウォリスの公式を用いて示される有名な公式としてスターリングの公式がある。
\[
n! \sim \sqrt{2 \pi n} \left(\frac{n}{e} \right)^n
\]
スターリングの公式は二項分布 \(B(n, p)\) の \(n\) が十分大きいとき正規分布に近似できる(ド・モアブルーラプラスの定理)ことを示す際に使われる。