初めに
本記事は、高校数学の数学Ⅰにおけるデータの分析で学ぶ四分位数、箱ひげ図についてまとめます。
四分位数
用語解説
四分位数
四分位数:データを値の小さい順に並べたとき、4等分する位置にくる値
小さいほうから第1四分位数、第2四分位数、第3四分位数といい、\(Q_1, Q_2, Q_3\)と表す。
\(Q_2\)は中央値である。\(Q_1, Q_3\)はそれぞれ下位のデータ、上位のデータの中央値とする。
| データの個数 | データの分け方 |
| 奇数個 | 〇〇〇〇〇〇〇 |
| 偶数個 | 〇〇〇〇〇〇 |
上の表において、〇が下位のデータであり、〇が上位のデータである。
範囲
\(\text{範囲} = \text{最大値} – \text{最小値}\)
四分位範囲・四分位偏差
\(\displaystyle{\text{四分位範囲} = Q_3 – Q_1}\)
\(\displaystyle{\text{四分位偏差} = \frac{\text{四分位範囲}}{2} = \frac{Q_3 – Q_1}{2}}\)
例題
問題
ある20人クラスで数学のテストを実施した。その結果、次のようなデータが得られた。このデータの範囲、四分位数、四分位範囲、四分位偏差を求めよ。
29 37 40 44 46 53 55 58 60 62 63 69 72 74 79 81 82 85 90 93 (点)
解答
範囲:\(93 – 29 = 64\)(点)
第1四分位数\(Q_1\)、第2四分位数\(Q_2\)、第3四分位数\(Q_3\)はそれぞれ
\[\begin{align}Q_1 &= \frac{46 + 53}{2} = 49.5 \text{(点)}\\ Q_2 &= \frac{62 + 63}{2} = 62.5 \text{(点)}\\ Q_3 &= \frac{79 + 81}{2} = 80 \text{(点)}\end{align}\]
となる。
四分位範囲:\(\displaystyle{Q_3 – Q_1 = 80 – 49.5 = 30.5}\)(点)
四分位偏差:\(\displaystyle{\frac{Q_3 – Q_1}{2} = \frac{30.5}{2} = 15.25}\)(点)
解説
第2四分位数\(Q_2\)は中央値です。今回はデータの値が偶数個なので、中央の2つの値の平均値が中央値となります。また、下位のデータと上位のデータは次のようになります。
- 下位のデータ: 29 37 40 44 46 53 55 58 60 62
- 上位のデータ:63 69 72 74 79 81 82 85 90 93
下位のデータの中央値が第1四分位数\(Q_1\)、上位のデータの中央値が第3四分位数\(Q_3\)なので、上記のように求められます。
中央値の求め方については、代表値の記事をご覧ください。
四分位偏差の意味について
偏差とは、基準値(平均値や中央値など)からの差をことを表します。
四分位偏差は
\[\frac{Q_3 – Q_1}{2} = \frac{(Q_3 – t) – (Q_1 – t)}{2}\]
と変形できるため、\(t\)を基準値とする偏差の平均を表していることがわかります。
箱ひげ図
用語解説
箱ひげ図
箱ひげ図:最小値、四分位数、最大値を表した図
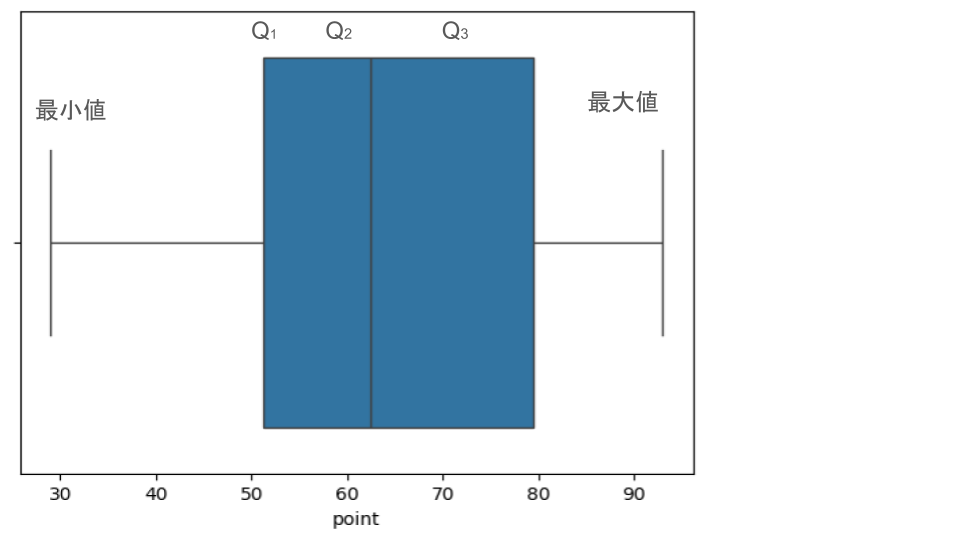
箱が四分位数を表しています。最小値から第1四分位数まで、第3四分位数から最大値までがひげのように見えるため、箱ひげ図と呼ばれています。
(補足)
- この図では、横に軸をとっていますが、縦に軸をとることもあります。
- 平均値を「+」で記入することもあります。
四分位数を用いた外れ値の検出
用語解説
外れ値
外れ値:他の値を比べて、大きく外れた値
外れ値の基準として四分位数を用いたものが教科書では紹介される。
データのとる値\(x\)において, 次の不等式を満たすものを外れ値という。
\[
x \leq Q_1 \ – \ 1.5(Q_3 \ – \ Q_1), \ Q_3 + 1.5(Q_3 \ – \ Q_1) \leq x
\]
すなわち、第1四分位数、第3四分位数から四分位範囲の\(1.5\)倍外側に外れた位置にある値を外れ値としている。