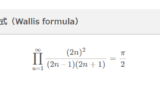初めに
本記事では、スターリングの公式を示す。ド・モアブル-ラプラスの定理(二項分布がサンプル数が十分大きいとき正規分布に近似できる)の証明に使われる公式です。
スターリングの公式(Stirling’s formula)
\[
n! ≒\sqrt{2 \pi n} \left( \frac{n}{e} \right)^n
\]
ここで \(f(n) ≒ g(n)\) は \(f(n)\) と \(g(n)\) が漸近的に等しいこと、すなわち \(\displaystyle{\lim_{n \rightarrow \infty} \frac{f(x)}{g(x)} = 1}\) を表す。
証明
証明には次の2つを使用します。
- ウォリスの公式
- 下に有界な単調減少数列は収束する
ウォリスの公式
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} = \frac{\pi}{2}
\end{align}\]
証明など詳細は下の記事をご覧ください。
下に有界な単調減少数列は収束する
\(\{a_n\}\) を広義単調減少、かつ下に有界な実数の数列とする。このとき、数列 \(\{a_n\}\) は収束する。
証明など詳細は下の記事をご覧ください。上に有界な単調増加列は収束することと合わせて証明しています。

証明
\( \displaystyle{\lim_{n \rightarrow \infty} \frac{n! e^n}{\sqrt{2 \pi n} n^n} = 1} \) を示せばよい。
収束することの証明
まず、\( \displaystyle{ a_n = \frac{n! e^n}{\sqrt{2 \pi n} n^n} } \) が \(n \rightarrow \infty \) で収束することを示す。
任意の自然数 \(n\) において、\(a_n > 0\) であるので下に有界であることは明らか。また、
\[\begin{align}
\log \frac{a_n}{a_{n + 1}} &= \log \frac{n! e^n (n + 1)^{n + 1} \sqrt{n + 1}}{n^n \sqrt{n} (n + 1)! e^{n + 1}} \notag \\
&= \log \frac{n + 1}{(n + 1) e} \left( 1 + \frac{1}{n}\right)^{n + \frac{1}{2}} \notag \\
&= \left( n + \frac{1}{2} \right) \log \left(1 + \frac{1}{n} \right) \ – \ 1
\end{align}\]
これを \(n\) で微分すると
\[\begin{align}
\frac{d}{dn} \left(\log \frac{a_n}{a_{n + 1}} \right) &= \log \left(1 + \frac{1}{n} \right) + \left( n + \frac{1}{2} \right) \cdot \frac{- \frac{1}{n^2}}{1 + \frac{1}{n}} \notag \\
&= \log \left(1 + \frac{1}{n} \right) \ – \ \frac{n + \frac{1}{2}}{n^2} \notag \\
\frac{d^2}{dn^2} \left(\log \frac{a_n}{a_{n + 1}} \right) &= – \frac{- \frac{1}{n^2}}{1 + \frac{1}{n}} \ – \ \frac{n(n + 1) \ – \ (n + \frac{1}{2})(2n + 1)}{n^2 (n + 1)^2} \notag \\
&= \frac{1}{2n^2 (n + 1)^2}
\end{align}\]
となる。\(n \geq 1\) において、\(\displaystyle{\frac{d^2}{dn^2} \left(\log \frac{a_n}{a_{n + 1}} \right) > 0}\) より \(n \geq 1\) で \(\displaystyle{\frac{d}{dn} \left(\log \frac{a_n}{a_{n + 1}} \right) }\) は単調増加である。また、\(\displaystyle{\lim_{n \rightarrow \infty} \frac{d}{dn} \left(\log \frac{a_n}{a_{n + 1}} \right) = 0}\) である。したがって、\(n \geq 1\) において \(\frac{d}{dn} \left(\log \frac{a_n}{a_{n + 1}} \right) < 0 \)であり、\(\displaystyle{\log \frac{a_n}{a_{n + 1}}}\) は単調減少である。また、
\[\begin{align}
\lim_{n \rightarrow \infty} \log \frac{a_n}{a_{n + 1}} &= \lim_{n \rightarrow \infty} \left(\left( n + \frac{1}{2} \right) \log \left(1 + \frac{1}{n} \right) – 1 \right)\notag \\
&= \lim_{n \rightarrow \infty} \left(\log \left(1 + \frac{1}{n} \right)^n + \frac{1}{2} \log \left(1 + \frac{1}{n} \right) \ – \ 1 \right) \notag \\
&= 1 + 0 \ – \ 1 \notag \\
&= 0 \notag
\end{align}\]
より \(\log \frac{a_n}{a_{n + 1}} > 0\) となる。よって、\(\{a_n\}\) は単調減少である。以上より数列 \(\{a_n\}\) は広義単調減少、かつ下に有界な数列であるため、収束する。
収束先が正の数であることの証明
次に \(\displaystyle{\lim_{n \rightarrow \infty} \frac{n! e^n}{\sqrt{2 \pi n} n^n} = A }\) としたとき、\(A > 0\) であることを示す。
まず、\(n \geq 1\) で次の不等式が成り立つことを示す。
\[
\log \frac{a_n}{a_{n + 1}} = \left( n + \frac{1}{2} \right) \log \left(1 + \frac{1}{n} \right) \ – \ 1 < \frac{1}{4n (n + 1)}
\]
これを示すには、
\[
h(n) := \frac{1}{4n(n + 1)} \ – \ \left(\left( n + \frac{1}{2} \right) \log \left(1 + \frac{1}{n} \right) \ – \ 1 \right) > 0
\]
を示せばよい。
\(\displaystyle{g(n) = \frac{1}{4n(n + 1)}}\) とおくと
\[\begin{align}
\frac{dg}{dn} (n) &= – \frac{1}{4} \cdot \frac{2n + 1}{n^2 (n + 1)^2} \notag \\
\frac{d^2 g}{dn^2} (n) &= – \frac{1}{4} \cdot \frac{2n^2 (n + 1)^2 \ – \ (2n + 1)(4n^3 + 6n^2 + 2n)}{n^4 (n + 1)^4} \notag \\
&= \frac{1}{4} \cdot \frac{6 n^3 + 12 n^2 + 8n + 2}{n^3 (n + 1)^4} \notag \\
&= \frac{1}{4} \cdot \frac{(n + 1)(6n^2 + 6n + 2)}{n^3 (n + 1)^4} \notag \\
&= \frac{1}{4} \cdot \frac{6 n^2 + 6n + 2}{n^3 (n + 1)^3} \notag
\end{align}\]
となる。よって、
\[\begin{align}
\frac{d^2 h}{d n^2} (n) &= \frac{d^2 g}{dn^2} (n) \ – \ \frac{d^2}{dn^2} \left(\log \frac{a_n}{a_{n + 1}} \right) \notag \\
&= \frac{1}{4} \cdot \frac{6 n^2 + 6n + 2}{n^3 (n + 1)^3} \ – \ \frac{1}{2n^2 (n + 1)^2} \notag \\
&= \frac{2n^2 + 2n + 1}{2n^3 (n + 1)^3} \notag \\
&= \frac{2(n + \frac{1}{2})^2 + \frac{1}{2}}{2n^3 (n + 1)^3} > 0
\end{align}\]
であり、\(\displaystyle{\frac{dh}{dn} (n)}\) は単調増加である。また、
\[\begin{align}
\lim_{n \rightarrow \infty} \frac{dh}{dn} (n) &= \lim_{n \rightarrow \infty} \left(\frac{dg}{dn} (n) \ – \ \frac{d}{dn} \left(\log \frac{a_n}{a_{n + 1}} \right) \right)\notag \\
&= \lim_{n \rightarrow \infty} \left(- \frac{1}{4} \cdot \frac{2n + 1}{n^2 (n + 1)^2} \ – \ \log \left(1 + \frac{1}{n} \right) \ – \ \frac{n + \frac{1}{2}}{n^2} \right) \notag \\
&= 0 \notag
\end{align}\]
より\(\displaystyle{\frac{dh}{dn} (n) < 0}\) であるため、\(h(x)\) は単調減少である。上記より \(\displaystyle{\lim_{n \rightarrow \infty} \log \frac{a_n}{a_{n + 1}} = 0}\) であったことに注意すると
\[\begin{align}
\lim_{n \rightarrow \infty} h(n) &= \lim_{n \rightarrow \infty} \left(\frac{1}{4n(n + 1)} – \log \frac{a_n}{a_{n + 1}} \right) \notag \\
&= 0 \ – \ 0 \notag \\
&= 0 \notag
\end{align}\]
となる。よって、\(h(n) > 0\) が成り立ち、
\[
\left( n + \frac{1}{2} \right) \log \left(1 + \frac{1}{n} \right) \ – \ 1 < \frac{1}{4n (n + 1)}
\]
が示せた。
いま、
\[
\log \frac{a_n}{a_{n + 1}} < \frac{1}{4n(n + 1)} = \frac{1}{4} \left( \frac{1}{n} \ – \ \frac{1}{n + 1}\right)
\]
より
\[\begin{align}
\log \frac{a_1}{a_n} &= \log \left(\frac{a_1}{a_2} \cdot \frac{a_2}{a_3} \cdots \frac{a_{n – 1}}{a_n} \right) \notag \\
&= \sum_{i = 1}^{n – 1} \log \frac{a_i}{a_{i + 1}} \notag \\
&< \sum_{i = 1}^{n – 1} \frac{1}{4} \left( \frac{1}{i} \ – \ \frac{1}{i + 1}\right) \notag \\
&= \frac{1}{4} \left( \left(1 \ – \ \frac{1}{2} \right) + \left(\frac{1}{2} \ – \ \frac{1}{3} \right) + \cdots + \left(\frac{1}{n \ – \ 1} \ – \ \frac{1}{n}\right) \right) \notag \\
&= \frac{1}{4} (1 \ – \ \frac{1}{n}) \notag \\
&< \frac{1}{4} \notag
\end{align}\]
となる。\(a_1 = \frac{e}{\sqrt{2 \pi}}\) より
\[\begin{align}
\log \frac{a_1}{a_n} < \frac{1}{4} & \Leftrightarrow \log a_1 – \log a_n < \frac{1}{4} \notag \\
& \Leftrightarrow \log \frac{e}{\sqrt{2 \pi}} \ – \ \log a_n < \frac{1}{4} \notag \\
& \Leftrightarrow \log a_n > \frac{3}{4} + \log \frac{1}{\sqrt{2 \pi}} \notag \\
& \Leftrightarrow \log a_n > \log \frac{e^\frac{3}{4}}{\sqrt{2 \pi}} \notag \\
& \Leftrightarrow a_n > \frac{e^\frac{3}{4}}{\sqrt{2 \pi}} \notag
\end{align}\]
である。したがって、任意の自然数 \(n\) において、\(a_n > 0\) がいえた。
収束先が1であることの証明
ウォリスの公式
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} = \frac{\pi}{2}
\end{align}\]
を用いて示す。
ウォリスの公式の左辺を変形する。
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} &= \frac{2^2}{1 \times 3} \cdot \frac{4^2}{3 \times 5} \cdots \notag \\
&= \lim_{n \rightarrow \infty} \frac{\{(2n)!!\}^2}{(2n – 1)!! (2n + 1)!!} \notag \\
\end{align}\]
となる。
\[\begin{align}
\frac{1}{(2n – 1)!!} &= \frac{1}{1 \cdot 3 \cdot 5 \cdots (2n \ – \ 1)} \notag \\
&= \frac{2 \cdot 4 \cdot 6 \cdots 2n}{(2n)!} \notag \\
&= \frac{2^n n!}{(2n)!} \notag \\
\frac{1}{(2n + 1)!!} &= \frac{1}{1 \cdot 3 \cdot 5 \cdots (2n + 1)} \notag \\
&= \frac{2 \cdot 4 \cdot 6 \cdots 2n}{(2n)! (2n + 1)} \notag \\
&= \frac{2^n n!}{(2n)! (2n + 1)} \notag
\end{align}\]
より
\[\begin{align}
\prod_{n = 1}^\infty \frac{(2n)^2}{(2n \ – \ 1)(2n + 1)} &= \lim_{n \rightarrow \infty} \frac{\{(2n)!!\}^2 (2^n n!)^2)}{\{(2n)!\}^2 (2n + 1)} \notag \\
&= \lim_{n \rightarrow \infty} \frac{2^{4n} (n!)^4)}{\{(2n)!\}^2 (2n + 1)} \notag \\
&= \lim_{n \rightarrow \infty} \frac{2^{4n}}{2n + 1} \left( \frac{n! e^n}{\sqrt{2 \pi n} n^n }\right)^4 \left( \frac{(2n)^{2n} \sqrt{2 \pi \cdot 2n}}{(2n)! e^{2n}} \right)^2 \frac{\pi n}{2^{4n}} \notag
\end{align}\]
と式変形できる。よって、
\[\begin{align}
\frac{A^4}{A^2} \lim_{n \rightarrow \infty} \frac{\pi n}{2n + 1} = \frac{\pi}{2}
\end{align}\]
より \(\displaystyle{\frac{\pi A^2}{2} = \frac{\pi}{2}}\) となる。\(A > 0\) より \(A = 1\) が示せる。